Lesson 2: Concentration

Part c: Percent by Mass and by Volume

Part a: Molarity
Part b: Dilution
Part c: Percent by Mass and by Volume
Part d: Solution Stoichiometry

 

What is Percent by Mass?

The concept of molarity as a concentration was introduced and detailed in Lesson 2a. But there are other means of expressing concentration besides molarity. Whatever means that is used, concentration provides information about the amount of solute and the amount of solution (or solvent).
 
Mass percent is another means of expressing the concentration of a solute in a solution. Mass percent indicates the fraction of the total mass of a solution that is contributed by the solute; the fraction is multiplied by 100 and expressed as a percentage. The mass percent formula is …

The denominator in the fraction is the total mass of the solution - the mass of solute(s) plus the mass of the solvent.
 
Suppose that a solution of ethanol is made by mixing 5.0 g of ethanol with 100.0 g of water. The mass percent of ethanol in the solution is …

 
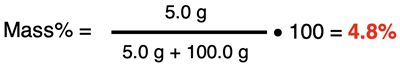
The frequent challenge in performing mass percent calculations is the denominator of the fraction - the mass of the solution. The mass of the solution is related to the volume of the solution by the density of the solution (if known). For aqueous solutions, a rough approximation is often made that the mass of the solvent can be found by assuming that the volume of water in the solution is equal to the volume of the solution. Combining this assumption with the value of water’s density (1.0 g/mL) allows one to determine the mass of the solvent. The following two examples demonstrate approaches to determining the mass of solution.
 
 

 

 

Example 1

Dewey Yurself is preparing a bottle of 1.0% Saline Solution by mixing table salt (NaCl) into distilled water. He has measured out exactly 1 cup of water (so he says, for what it is worth). He has used Google to determine that there are 236.6 mL in one cup. What mass of NaCl should he add to this water in order to make a 1.0% NaCl solution?
 
 

Solution:

The solute is NaCl. We wish to know its mass. We represent its mass (in grams) by the symbol X. The solvent is water. We know there are 236.6 mL of water; using 1.00 g/mL as the density of water, the mass of the solvent is 236.6 g. The mass of the solution is the mass of the water plus the mass of the NaCl. We will represent this by 236.6 + X. The mass percent equation can be set up as

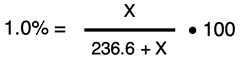
Algebra is required to solve for X. We will divide both sides of the equation by 100 to get

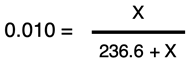
By multiplying both sides of the equation by the quantity (236.6 + X) we can eliminate the denominator on the right side of the equation. The result is:

0.010 • (236.6 + X) = X

Multiplying the two terms in the parenthesis by 0.010 yields

2.366 + 0.010•X = X

Subtracting 0.010•X from both sides allows us to group the X terms on one side with a coefficient on the opposite side:

2.366 = X - 0.010•X

We can simplify right side of this equation, leading to

2.366 = 0.990•X

Dividing through both sides of the equation by 0.990 allows us to determine X as

X = 2.4 grams
(rounded to the first decimal place from 2.3898… grams)

 
 
 

Example 2

Vinegar is an aqueous solution of acetic acid (HC₂H₃O₂). It is 5.00% by mass acetic acid and has a density of 1.006 g/mL. Determine the mass of acetic acid in a 500.0 mL sample of vinegar.
 
 

Solution:

Acetic acid is the solute. We wish to determine its mass. We represent its mass (in grams) by the symbol X. We know the volume of the solution and the density of the solution. The mass of the solution can be determined from this information:

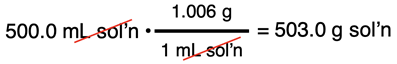
We can now set up our mass percent formula with known values:

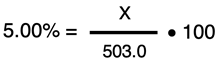
The algebraic steps to solve for X are similar to those performed in Example 1. We will divide through both sides of the equation by 100 to get

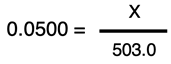
Multiplying both sides of the equation by 503.0 allows us to determine the value of X:

X = 0.0500 • 503.0 = 25.2 g
(rounded from 25.15 to three significant digits)
 
 

 

 

Converting from Molarity to Mass Percent

Conversions are commonly made between concentration units. For instance, it is often necessary to convert from the molarity of a solution to its mass percent. The starting point for such conversions involves assuming a sample size. For conversions from molarity to mass percent, a sample size of 1.000 L is rather convenient. This allows one to quickly determine the moles of solvent in the 1.000 L of solution. Knowing the identity of the solute, and thus the molar mass, allows one to determine the mass of solute. The density of the solution can be used to determine the mass of the solution from the volume of the solution. Example 3 illustrates how to perform such a conversion.
 
 
 

Example 3

A 6.00 M aqueous solution of HCl has a density of 1.097 g/mL. Determine the mass percent of HCl in the solution.
 
 

Solution:

Our starting point will be to assume that we have 1.000 L of solution. Making this assumption allows us to determine the mass of solute and the mass of solution. The solute is HCl. There will be 6.00 mol of HCl in this assumed volume. The molar mass of HCl (36.461 g/mol) can be used to determine the mass of HCl.

The mass of solution can be determined using the density of the solution.

With the mass of solute and the mass of solution known, we can calculate the mass percent value:

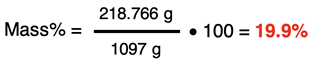
(rounded to three significant digits)

 
 

 
 

Converting from Mass Percent to Molarity

Conversions in the opposite direction - from mass percent to molarity - are also quite common. These conversions require a starting point. The most feasible option is to assume a sample size of 100.0 g of solution. This allows one to quickly determine the mass of the solute in the sample. The moles of solute can be calculated from the mass of solute using the molar mass. Density information is used to determine the volume of the solution. Molarity can always be calculated from the moles of solute and the volume of solution. Example 4 illustrates how to perform such a conversion.
 
 

Example 4

A bottle in the “Danger! Strong Oxidixers!” cabinet of the Chemistry storeroom reads “30.0% H₂O₂ in Water.” The density of the solution is 1.112 g/mL. Determine the molar concentration of H₂O₂.
 
 

Solution:

Our starting point will be to assume that we have 100.0 g of solution. Making this assumption allows us to determine the moles of solute and the volume of solution in liters. The solute is H₂O₂. Since the solution is 30.0% H₂O₂ by mass, there will be 30.0 g in the 100.0 g of solution. The molar mass of H₂O₂ is 34.0147 g/mol. This can be used to determine the moles of H₂O₂.

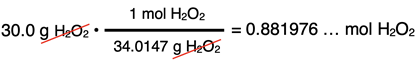
The density of the solution is given as 1.112 g/mL. Having assumed 100.0 g of solution allows us to determine the volume:

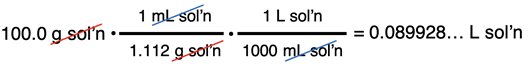
The molarity can now be calculating using the moles of solute and the volume of solution:

 

(answer is rounded to three significant digits from 9.80752… M)

 
 
 

Volume Percent

A related means of expressing the concentration of a solution is the use of volume percent. Like mass percent, the volume percent indicates the fraction of the total volume of a solution that is attributable to the solute; the fraction is multiplied by 100 and expressed as a percentage. The volume percent formula is …

Volume percent expressions are most common for situations in which the solute and the solvent are both liquids. Mass percent is more common for solutions involving solid solutes.
 
 
 
 

Before You Leave

• Download our Study Card on Percent by Mass. Save it to a safe location and use it as a review tool.
• When it comes to solving Chemistry problems, our Calculator Pad is an awesome location for perfecting your skills. The following problem set coordinates well with Lesson 2c: Problem Set MS3: Concentration – Mass Percent
• The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.

 
 
 
 

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
1. Suppose that 15.25 g NaCl are dissolved in 198.37 g H₂O. What is the mass percent of NaCl in the solution?

 
 

2. In preparation for her St. Patrick’s Day demonstration, Mrs. Symone added 50.0 g of boric acid (H₃BO₃) crystals to 250.0 mL of methanol. (Don’t do this at home. It should only be done by trained professionals like Mrs. Symone.) The density of methanol is 0.792 g/mL. Determine the mass percent of boric acid in the solution.


 
 
​
3. During a Chemistry lab, Maibee Abase prepares a solution by dissolving 26.1 g of NaOH into a 250.0 mL volumetric flask … filled to the 250.0-mL mark with water. Determine the mass percent of NaOH in the solution. (Assume that 250.0 mL of water were needed to make the solution.)


 
 
​
4. Mr. Wiggly (Physics teacher) was having a conversation with Mrs. Mandochino just prior to her AP Chemistry class. Reportedly, Mr. Wiggly was preparing a “fantastic, incredible, and awesome five-star refraction demonstration” for one of his classes. He needed Mrs. Mandochino’s help preparing the solution. The directions called for a 2.00-L aqueous solution of 25.0% sucrose (table sugar, C₁₂H₂₂O₁₁). The density of the solution is 1.105 g/mL. Mr. Wiggly is asking Mrs. Mandochino about how much sucrose and how much water to mix together. Class started and Mrs. Mandochino passed the problem on to her students, promising a Dataway! sticker to the first student to determine the details. It’s your turn to solve it. Go for the big reward!


 
 
​
5. Claire Synisus worked a job this past summer for Mean to Clean, LLC. Claire recalls there being a large bottle of commercial grade aqueous ammonia in the warehouse that was labeled “29.9% NH₃ (by mass); density = 0.896 g/mL”. Determine the molarity of NH₃ for this solution.


 
 ​