 Snell's Law
Snell's Law
Resource:
The Science Reasoning Center: Snells Law
Grade Level: High School
Description:
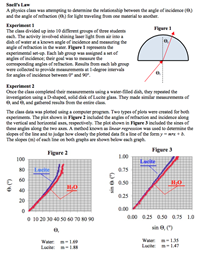
This passage describes two experiments in which students investigate the effect of the angle of incidence upon the angle of refraction. Data is collected for the air-water and the air-Lucite boundary and presented as an angle of incidence vs. angle of refraction graph and as a sine of the angle of incidence vs. sine of the angle of refraction graph. Questions target a student's ability to understand the design of an experiment, to predict the outcome of performing the experiment in a different manner, to identify the qualitative relationship among variables, to combine two or more data presentations in order to develop appropriate conclusions, and to use a model in order to analyze information and draw appropriate conclusions.
This activity aligns with the three dimensions of the Next Generation Science Standards in the manner described below:
| Patterns: Empirical evidence is needed to identify patterns. |
This passage describes two experiments in which students investigate the effect of the angle of incidence upon the angle of refraction for laser light. Data is collected for an air-water and an air-Lucite boundary. Students make meaning of this collected data by analyzing two graphs—angle of incidence vs. angle of refraction as well as sine of the angle of incidence vs. sine of the angle of refraction. As they do, several patterns emerge. One such relationship shows how the second graph ‘linearizes’ the data giving rise to a slope that is equal to the index of refraction of the refractive medium. Questions at the close of this passage point students to explore this and other patterns. |
| Structure and Function: The functions and properties of natural and designed objects and systems can be inferred from their overall structure, the way their components are shaped and used, and the molecular substructures of its various materials. |
Questions at the end of the passage introduce the index of refraction values for the three substances (air, water, Lucite glass) used in this experiment. As students consider these indices, they recognize that this value is an indicator of the relative speed at which light travels within a material. Students are asked to infer relationships between the amount of bending that occurs and index of refraction. Students can also infer that this quantity is in some way connected to the properties of the substance itself that are most likely determined at the molecular level. |
| Planning and Carrying Out Investigations: Plan an investigation or test a design individually and collaboratively to produce data to serve as the basis for evidence in building/revising models, supporting explanations for phenomena, or testing solutions to problems. Consider possible confounding variables and ensure variables are controlled. |
Two end-of-passage questions specifically address a student’s ability to understand the design of the experiments performed. One question asks students to use the context of the experimental description and the collected data to identify the purpose of the experiments, which is not explicitly stated. A second question helps students wrestle with why the experimenters prepared the second graph (sine angle incidence vs. sine angle refraction), which uses the same raw data as the first graph. As they arrive at an answer to this second question, students see how a new data representation serves as the basis for revising a refraction model. |
| Engaging in Argument from Evidence: Make and defend a claim based on evidence about the natural world that reflects scientific knowledge, and student-generated evidence. |
Several questions at the end of the passage target a student's ability to engage in argument from evidence. Student are particularly asked to predict the outcome of performing the experiment in a different manner, to identify the qualitative relationship among variables, to combine two or more data presentations in order to develop appropriate conclusions, and to use a model in order to analyze information and draw appropriate conclusions. |
| Using Mathematical and Computational Thinking: Use mathematical representations of phenomena or design solutions to support and revise explanations. |
As students analyze data for the air-water and the air-Lucite scenarios, they encounter the non-linear graph of angle of incidence vs. angle of refraction for each interface. They notice that the experimenters then produced a sine of the angle of incidence vs. sine of the angle of refraction graph for each interface—a graph that yields a linear relationship. Students are asked several questions related to why it was important to make this second graph. As they explore explanations, students come to realize that only the sine graph produces a linear relationship which in turn allows the experimenter to write a mathematical model (equation) that scientists know as Snell’s Law. |
Associated Reading from The Physics Classroom
Other Supporting Pages at The Physics Classroom:
View Infographic.
(Coming Soon)
Search the NGSS Corner
Maybe you're looking for something really specific that pertains to a desired topic and emphasizes one or more of the listed NGSS dimensions. Why not try a search of this section of our website? Simply select from one or more of the pull-down menus and click Search This page will reload and a collection of possibilities will be displayed in this section of the page and sorted by relevancy.