Vectors: Properties and Operations - Complete Toolkit
Objectives
-
To understand that a vector is a quantity that has a magnitude and direction and be able to graphically represent a vector using a scaled diagram and the counter-clockwise from east convention of direction.
-
To add vectors using a head-to-tail addition method and a scaled vector addition diagram and be able to identify the magnitude and direction of the resultant.
-
To add right-angle vectors, using the Pythagorean theorem to determine the resultant magnitude and trigonometric functions to determine the resultant direction.
-
To resolve vectors into components and to use the component method in order to add two or more non-perpendicular vectors in order to determine the resultant.
-
To understand that perpendicular components of motion are independent of each other and to use such an understanding to solve relative velocity problems such as riverboat problems.
Readings from The Physics Classroom Tutorial
-
The Physics Classroom Tutorial, Motion and Forces in Two Dimensions Chapter, Lesson 1
http://www.physicsclassroom.com/class/vectors/Lesson-1/Vectors-and-Direction
Interactive Simulations
-
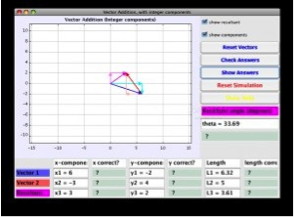 Boston University EJS: Vector Addition w/Integer Components
Boston University EJS: Vector Addition w/Integer Components
Good choice to give beginners practice in 2D vector addition. It’s relatively simple, as the x and y components of each vector are integers. Given the magnitude and direction of two vectors, students determine the x and y components, the length of each, and resultant vector sum. Click “Check Answers” to get immediate feedback; click “Show Answers” to display correct responses.
-
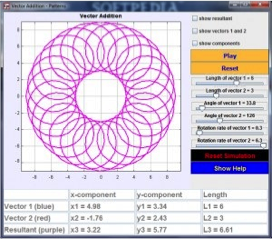 Boston University (EJS) Simulation: Vector Addition and Pattern
Boston University (EJS) Simulation: Vector Addition and Pattern
Kids will have fun with this simulation, which illustrates the tip-to-tail method of adding vectors. As students adjust lengths and angles of two vectors, the resultant vector and components are displayed. BUT WAIT. Students can also set rotation rates and watch the vectors spin, tracing out interesting patterns on the screen.
-
 Boston University EJS - Vector Addition
Boston University EJS - Vector Addition
Students who have mastered vector addition with integers can move up to this simulation, which introduces vectors with non-integer lengths.
-
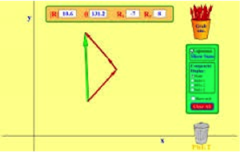 PhET Simulation: Vector Addition
PhET Simulation: Vector Addition
This interactive model lets students drag vectors onto a grid, change their length and angle, and sum them together. The magnitude, angle, and x/y components of each vector are automatically displayed in several formats. For beginning learners, we suggest using one or both of the PhET Teacher-Contributed Lessons (see links directly below)
PhET Vectors Lab Guide
http://phet.colorado.edu/en/contributions/view/3140
This is a student guide created specifically for use with the simulation “Vector Addition”. It provides explicit instructions on how to use the simulation, then presents a short assignment for using the model to calculate resultant vectors. Allow about 30 minutes. (86 kb Word document)
Virtual Vector Lab
http://phet.colorado.edu/en/contributions/view/3047
This student guide, created by a high school teacher, provides structured guidance for students as they use the PhET simulation “Vector Addition”. It gives detailed directions for using the simulation and scaffolded support for the tip-to-tail method and the Pythagorean Theorem. Allow two class periods.
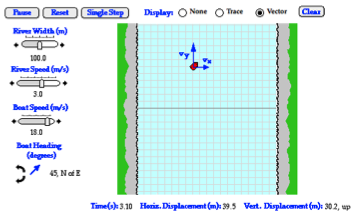
-
The Riverboat Simulator
This simulation from The Physics Classroom’s Shockwave Physics Studios allow the user to vary the speed and direction of a boat crossing a river and the river speed and width in order to explore the effect of a variable on the time to cross the river and the distance traveled downstream. Comes with a proposed activity sheet: http://www.physicsclassroom.com/shwave/rboatdirns.cfm.
Video and Animations
-
 Physlet Physics: Vector Decomposition
Physlet Physics: Vector Decomposition
Very simple applet that lets you drag a single vector around the coordinate grid. It displays changing values of x and y components, magnitude, and direction as the vector moves. It was designed to support students as they learn to “decompose” a vector into component form, building a foundation to understand the reasoning behind the mathematics of vector quantities.
-
 University of Arkansas Physics Department: Vector Calculator
University of Arkansas Physics Department: Vector Calculator
We like this tool for beginners because you can’t enter components manually. The tool displays a coordinate plane with a grid of 10 square units. Click anywhere in the grid to create a blue vector, then click again to create a red vector. As you click or drag, the tool calculates the components, magnitude, and direction of the vectors. Click “Add” and watch as the parallelogram is constructed (sum vectors are displayed alongside). Clicking and dragging within the grid gives students a way to get a feel for why vector math works.
-
 Physlet Physics Exploration: Addition of Displacement Vectors
Physlet Physics Exploration: Addition of Displacement Vectors
To apply vector quantities, let your students try this animated problem. It starts with a red dot representing an airplane that ascends for 8 seconds at take-off. The task is to drag a second vector with a given displacement, then draw the resultant vector. (This exercise is available as an interactive animation or as a printable worksheet.)
-
 Pfun Science: How to Find the Resultant of Three or More Vectors
Pfun Science: How to Find the Resultant of Three or More Vectors
This 15-minutevideo provides a very, very thorough explanation of how to find the resultant of 3 vectors – both graphically and algebraically. Could work well as part of a flipped lesson.
-
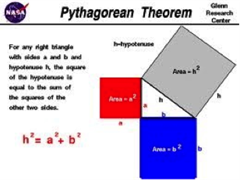 NASA Glenn Research Center: Pythagorean Theorem Animation
NASA Glenn Research Center: Pythagorean Theorem Animation
Sometimes it helps beginners to explore how a geometric proof was constructed. This animation from NASA uses geometric overlays to show why the Pythagorean Theorem works. Background information on the Theorem and its historical use is included.
Labs and Investigations
-
The Physics Classroom, The Laboratory, Map Lab
Students use a map (local, state, national) to analyze the mathematical relationships between the displacements of the individual legs of a two-legged and three-legged trip to the overall displacement.
-
The Physics Classroom, The Laboratory, As the Crow Flies Lab
Students walk to an assigned location in the school, measuring the displacements along each leg of the walk. They use the individual displacements to determine the magnitude and direction of the resultant displacement to the assigned location.
-
The Physics Classroom, The Laboratory, Where Am I? Lab
Students are given three vectors that lead to an unknown location in the school. Students must resolve each vector into a set of north-south and east-west displacements so they can walk out the path through the hallway to the destination. Students must then identify the unknown location (e.g., Room 332) and determine the overall resultant.
-
The Physics Classroom, The Laboratory, Road Trip Lab
Students are provided a regional or national map with a starting location and three displacement vectors. A scale is used to determine where the three displacements – added consecutively – lead to. Students identify the final destination and use vector addition to determine the resultant displacement.
-
The Physics Classroom, The Laboratory, Crossing the River Lab
Students use a riverboat simulator to determine the effect of varying boat speed, river speed and river width upon the time to cross the river and the distance traveled downstream.
Link: http://www.physicsclassroom.com/lab#vp
Demonstration Ideas
-
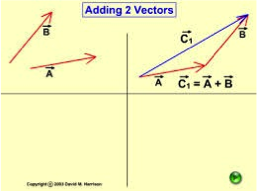 University of Toronto: Adding Two Vectors Animation-Based Demonstration
University of Toronto: Adding Two Vectors Animation-Based Demonstration

This simple but elegant simulation illustrates the commutative property of vector addition. It would make a good classroom demo or springboard for discussion of why, given two vectors in a plane, the sum will be the same in either way you connect a tip to a tail.
-
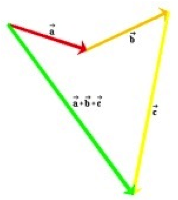 University of Calgary Physics Department: Vector Animations
University of Calgary Physics Department: Vector Animations
If you have patience, this collection offers a treasure trove of animated exercises relating to vector operations. It’s assembled in a modular format consisting of interactive models, explanations, and sample assessments. Animated screens walk the student step-by-step through the basics of vector addition, subtraction, resolution, dot products, and cross products. The directory isn’t really intuitive ... when in doubt, click on the files titled “Simulate”.
-
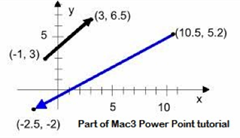 Vectors for Physics and Calculus Students: Mac3 Project
Vectors for Physics and Calculus Students: Mac3 Project

This unique resource is the brainchild of a collaboration of physics and mathematics instructors who aim to tackle “the problem” of a lack of cohesion between how vector operations are taught in physics vs. mathematics courses. No wonder students are confused when vector notations, units, and descriptions vary from one discipline to the other. The link takes you to the shorter presentation of “The Problem”, plus a 45-page presentation for use in the classroom.
Minds On Physics Internet Modules:
The Minds On Physics Internet Modules are a collection of interactive questioning modules that target a student’s conceptual understanding. Each question is accompanied by detailed help that addresses the various components of the question.
-
Vectors and Projectile Module, Ass’t VP1 - Direction of Vectors
-
Vectors and Projectile Module, Ass’t VP2 - Vector Addition Diagrams
-
Vectors and Projectile Module, Ass’t VP3 - Vector Addition Applications
-
Vectors and Projectile Module, Ass’t VP4 - Adding Right Angle Vectors
-
Vectors and Projectile Module, Ass’t VP5 - Vector Components
-
Vectors and Projectile Module, Ass’t VP6 - Velocity and River Boats
Link: http://www.physicsclassroom.com/mop
Concept Building Exercises:
-
The Curriculum Corner, Vectors and Projectiles, Vector Representation
-
The Curriculum Corner, Vectors and Projectiles, Addition of Vectors
-
The Curriculum Corner, Vectors and Projectiles, Vector Resolution and Vector Addition
-
The Curriculum Corner, Vectors and Projectiles, Vector Addition by Components
-
The Curriculum Corner, Vectors and Projectiles, Relative Velocity - Riverboat Problems
Link: http://www.physicsclassroom.com/curriculum/vectors
Problem-Solving Exercises:
-
The Calculator Pad, Vectors and Projectiles, Problems #1 - #20
Link: http://www.physicsclassroom.com/calcpad/vecproj
Real Life Connections:
-
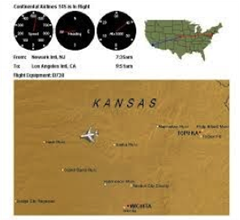 CIESE Real-Time Data Project: Navigational Vectors
CIESE Real-Time Data Project: Navigational Vectors

Do your students ask, “When will we ever use this?” This project-based unit can help bridge the gap between vector concepts and use of vector operations by real people in authentic situations. Activities (which can be parsed out) include reading real-time weather maps, tracking airplanes flying in U.S. skies, calculating vector components, analyzing effects of wind velocity, and completing training similar to a private pilot certification program.
-
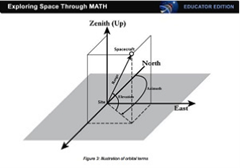 NASA Dryden Flight Research Center: Space Vectors
NASA Dryden Flight Research Center: Space Vectors

This complete lesson was developed for pre-calc students who have completed a course in trigonometry. It introduces vectors in 3 dimensions, thus requires prior knowledge of spherical coordinates, azimuth, elevation, range, and vector notation. Students will use Google Earth to find their school, using NASA’s naming conventions for longitude & latitude. Then students will use spherical coordinates and vector addition to find position coordinates of the international space shuttle with respect to the Earth’s center and Dryden Flight Research Center.
Common Misconception:
-
The Order of Vector Addition Does Not Matter
Students are often under the impression that the resultant of two or more vectors depends upon the order in which they are added. This misconception can be easily dispelled by simply having students measure out two right-angled vectors in the two different orders. The destination is the same despite the order in which they are added.
-
Perpendicular Components
The independence of perpendicular components of motion is an important principle derived from a unit on vectors that will foster a better understanding of projectile motion. An alteration in a north-south component of motion will not affect an east-west component of motion. This principle is most easily reinforced by a study of the motion of a riverboat heading straight across a river. A change in the riverboat speed does not affect the distance that the boat travels down the river. In a similar manner, a change in the horizontal velocity of a projectile does not affect the time required for the projectile to fall to the ground. Perpendicular components of motion are independent of each other.
Related PER (Physics Education Research)
-
University of Monterrey Physics Education Research Group
This article from the University of Monterrey Physics Education Research group discusses results of a large study gauging the understanding of vector concepts among 2,000+ college students. Areas of strength included representing x and y components, calculating magnitude, finding vector sums, and calculation of dot and cross products using given equations. However, even after 3 courses in physics, the students showed surprising weakness in calculating vector direction, subtraction of vectors in 2D, and geometric interpretations of dot and cross products.
-
 Physics Education Research Conference Proceedings Annotated Collection
Physics Education Research Conference Proceedings Annotated Collection
 Student difficulties with vector concepts are often pervasive, extending persistently beyond high school through multiple undergraduate courses in physics and engineering. In the past two years, PER (physics education research) has focused more on error patterns and promising interventions. Click the link below for an annotated collection of the most relevant research publications we found for you. (All are in condensed formats and available for free download.)
Student difficulties with vector concepts are often pervasive, extending persistently beyond high school through multiple undergraduate courses in physics and engineering. In the past two years, PER (physics education research) has focused more on error patterns and promising interventions. Click the link below for an annotated collection of the most relevant research publications we found for you. (All are in condensed formats and available for free download.)
-
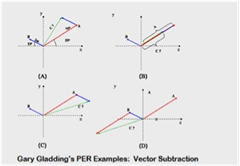 PER Examples: Vector Subtraction Interactive Homework Problem
PER Examples: Vector Subtraction Interactive Homework Problem
 Great interactive problem to help students overcome difficulties with vector subtraction. It takes learners step-by-step through a conceptual analysis, then proceeds to a strategic analysis with explicit support for setting up equations appropriately. Finally, the learner will perform the math with scaffolded help available at each waypoint. Questions are carefully crafted to promote success without spoon-feeding answers.
Great interactive problem to help students overcome difficulties with vector subtraction. It takes learners step-by-step through a conceptual analysis, then proceeds to a strategic analysis with explicit support for setting up equations appropriately. Finally, the learner will perform the math with scaffolded help available at each waypoint. Questions are carefully crafted to promote success without spoon-feeding answers.
Standards:
A. Next Generation Science Standards (NGSS)
Crosscutting Concepts
Scale, Proportion, and Quantity
-
High School: Algebraic thinking is used to examine scientific data and predict the effect of a change in one variable on another.
Science and Engineering Practices
Practice #2: Developing and Using Models
-
Use a model to predict the relationships between systems or between components of a system.
-
Use a model to provide mechanistic accounts of phenomena.
Practice #3: Planning and Carrying Out Investigations
-
Plan and conduct an investigation individually and collaboratively to produce data to serve as the basis for evidence, and in the design: decide on types, how much, and accuracy of data needed to produce reliable measurements and consider limitations on the precision of the data (e.g., number of trials, cost, risk, time), and refine the design accordingly.
Practice #4: Analyzing and Interpreting Data
-
Analyze data using tools, technologies, and/or models (e.g., computational, mathematical) in order to make valid and reliable scientific claims or determine an optimal design solution.
-
Analyze data using computational models in order to make valid and reliable scientific claims.
Practice #5: Using Mathematics and Computational Thinking
-
Use mathematical representations of phenomena to describe explanations.
-
Create a computational model or simulation of a phenomenon, process, or system
-
Use mathematical representations of phenomena to support and revise explanations
Practice #8: Obtaining, Evaluating, and Communicating Information: High School
-
Communicate scientific information about phenomena in multiple formats (including orally, graphically, textually, and mathematically)
B. Common Core Standards for Mathematics – Grades 9-12
Standards for Mathematical Practice:
-
MP.2 – Reason abstractly and quantitatively
-
MP.4 – Model with mathematics
-
MP.6 – Attend to precision
High School Algebra: Seeing Structure in Expressions
-
A-SSE.A.b: Interpret complicated expressions by viewing one or more of their pairs as a single entity
-
A-SSE.2: Use the structure of an expression to rewrite it.
High School Algebra: Creating Equations
-
A-CED.2 Create equations in two or more variables to represent relationships between quantities, graph equations on coordinate axes with labels and scales
-
A-CED.4 Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations
High School Functions: Interpreting Functions
-
F-IF.4: For a function that models a relationship between two quantities, interpret key features of graphs and tables in terms of the quantities, and sketch graphs showing key features given a verbal description of the relationship.
-
F-IF.5: Relate the domain of a function to its graph and, where applicable, to the quantitative relationship it describes.
High School Functions: Building Functions
-
F-BF.4.b: Verify by composition that one function is the inverse of another.
-
F-BF.5: Understand the inverse relationship between exponents and logarithms and use this relationship to solve problems involving logarithms and exponents.
High School Functions: Linear, Quadratic, and Exponential Models
-
F-LE.5: Interpret the parameters in a linear or exponential function in terms of a context.
High School Functions: Trigonometric Functions
-
F-TF.1: Understand radian measure of an angle as the length of the arc on the unit circle subtended by the angle.
-
F-TF.2: Explain how the unit circle in the coordinate plane enables the extension of trigonometric functions to all real numbers, interpreted as radian measures of angles traversed counterclockwise around the unit circle.
-
F-TF.3: Use special triangles to determine geometrically the values of sine, cosine, tangent and use the unit circle to express the values of sine, cosine, and tangent in terms of their values for x, where x is any real number.
C. Common Core Standards for English/Language Arts (ELA) – Grades 9-12
Reading Standards: Science and Technical Subjects – Key Ideas and Details
-
RST.11-12.2 – Determine the central ideas or conclusions of a text; summarize complex concepts, processes, or information presented in a text by paraphrasing them in simpler but still accurate terms.
-
RST.11-12.3 – Follow precisely a complex multistep procedure when carrying out experiments, taking measurements, or performing technical tasks; analyze the specific results based on explanations in the text.
Science and Technical Subjects – Integration of Knowledge and Ideas
-
RST.11-12.9 – Synthesize information from a range of sources (e.g., texts, experiments, simulations) into a coherent understanding of a process, phenomenon, or concept, resolving conflicting information when possible.
Science and Technical Subjects – Range of Reading and Level of Text Complexity
-
RST.11-12.10 By the end of grade 12, read and comprehend science/technical texts in the grades 11-CCR text complexity band independently and proficiently.