Light Waves: Extra Problems

Problem Set A

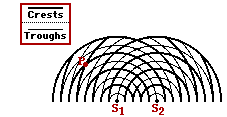Problem 1:

The diagram at the right represents the interference pattern created by two water waves. The waves were created by two vibrating objects which oscillate up and down in phase at the same frequency. Point P on the pattern is a distance of 23.27 cm from S₁ and 34.37 cm from S₂. Determine the wavelength (in cm) of the water waves.

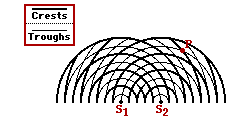Problem 2:

The diagram at the right represents the interference pattern created by two water waves. The waves were created by two vibrating objects which oscillate up and down in phase at the same frequency. Point P on the pattern is a distance of 75.8 cm from S₁ and 47.5 cm from S₂. Determine the wavelength (in cm) of the water waves.

Problem 3:

A point on the fourth nodal line is a distance of 89.6 cm from the furthest source. The wavelength of the waves is 10.2 cm. What is the distance (in cm) from the same point to the nearest source?

Problem 4:

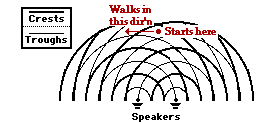Two audio speakers produce sound waves in phase. The sound travels through the room and interferes to create a pattern. A person starts at a location midway between the speakers and walks parallel to the line which connects the speakers until she is standing at the first location of minimal loudness. The sound waves travel through the room at 362 m/s and their frequency is 212 Hertz. If she is standing 34.4 meters from the nearest speaker (when at the first point of minimum loudness, then how far (in meters) is she from the furthest speaker?

Problem 5:

A radio station uses two attenas to broadcast a signal at 808 kiloHertz. The radio waves emanate from the attenas in phase and travel at the speed of light. The occupants of a home are located 279 kilometers from the nearest attena and have the worst possible reception when tuned to this station. What is the likely minimum distance (in kilometers) from the home to the second attena? Enter your answer to the third decimal place.

Problem 6:

It is known that signals from radio and television stations can reflect off airplanes and mountains and interfere with the signal traveling directly from the station to a home. Suppose that a 6355.9 kiloHertz signal reflects off an airplane located 354 meters above the receiver and destructively interferes with a signal sent directly from a distant station. What next highest plane elevation (in meters) would result in destructive interference? (Assume that the wave does not undergo a phase change upon reflection off the plane.)

Problem 7:

Monochromatic light falls on a screen 2.54 meters from two slits spaced 1.51 mm apart. The first and the second bright bands are found to be 0.606 mm apart. What is the wavelength (in nanometers) of the light?

Problem 8:

If the distance between two slits is 0.0606 millimeters and the distance to a screen 4.56 meters, find the spacing (in millimeters) between the first and second-order bright fringes for light with a 666 nm wavelength.

Problem 9:

A pair of narrow, parallel slits separated by 0.458 mm are illuminated by the green component from a mercury vapor lamp (wavelength = 546.1 nm). The interference pattern is projected onto a screen 3.06 meters from the plane of the parallel slits. Calculate the distance (in millimeters) from the central maximum to the 10th bright band of the pattern.

Problem 10:

(Referring to the previous problem.) What is the distance (in millimeters) between the 7th and the 12th dark band in the pattern (on the same side of the central maximum)?

Problem 11:

A double slit with a spacing of 0.095 millimeters between the slits is 4.579 meters from a screen. If yellow light of wavelength 570 nm strikes the double slits, what is the separation (in millimeters) between the central bright band and the first bright band on either side of the central band?

Problem 12:

(Referring to the previous problem.) If blue light of wavelength 410 nm strikes the same double slit and lands on the same screen, then what is the separation distance (in millimeters) between the 5th bright band and the 12th dark band of the pattern.

Problem 13:

A physics class uses a laser with a known wavelength of 674 nm in a double-slit experiment. The slit separation is unknown. A student places the screen 1.61 meters from the slits and finds the first antinode to be located 81.4 mm from the central anti-node. What is the slit separation (in micrometers)? (10^6 micrometer = 1 meter)

Problem 14:

(Referring to the previous problem). If the distance from the slits to the screen is increased by a factor of 9, then what would be the new distance (in millimeters) from the first antinode to the central bright spot?

Problem 15:

A warehouse on a dock has two open doors. A boat sounds its horn from across the river. To person A, the sound is loud and clear; he is located directly between the two open doors near the back wall of the wharehouse. To person B, the sound is barely audible. The principal wavelength of the sound waves is 3.64 meters. Assuming that person B is at the position of the first minimum and near the back wall of the wharehouse, determine the distance (in meters) between the doors, center to center. Persons A and B are located 161 meters from the wall of the warehouse and are spaced 27.4 meters apart.

Problem 16:

Light of wavelength 647 nm falls on two slits spaced 0.457 mm apart. What is the required distance (in meters) from the slits to a screen if the spacing between the first and the second dark fringes is to be 9.19 mm?

Problem 17:

A physics teacher is using two audio speakers to demonstrate sound interference. The speakers are located 4.34 meters apart and playing a frequency of 446 Hertz. (Assume a speed of sound of 345 m/s.) Students are sitting in seats in the same row in an auditorium. The seats are spaced 116.2 centimeters apart and every third student is sitting in a position of destructive interference. What is the perpendicular distance (in meters) from the row of students to the line connecting the speakers?

Problem 18:

Young's experiment is performed with laser light. The separation distance between the slits is 0.707 mm and the interference pattern on a screen 7.13 meters away shows the first maximum is at a distance of 6.09 mm from the center of the pattern. What is the wavelength (in nanometers) of the light?

Problem 19:

One of the bright bands in Young's interference pattern is located 43.3 mm from the central maximum. The screen is 201 cm from the pair of slits that serve as sources. The slits are 0.406 mm apart and are illuminated by the blue light from a hydrogen discharge tube (wavelength = 486 nm). How many bright lines are observed between the central maximum and the bright band at the 43.3-mm position? Do not include the central band in your count but do include the band at the 43.3-mm position in the count. 

Problem 20:

Monochromatic light with a wavelength of 636 nanometers passes through two slits and produces a two-point source interference pattern on a screen located 18.5 meters away. The fourth dark band is located 9.81 centimeters from the central anti-node. Determine the slit separation (in micrometers).