Wave Basics: Extra Problems
The problems below are provided as additional problems to
the original set of 29 Waves problems. Just like problems in the original set, these problems consist of a problem, an answer (revealed by clicking a link), an audio guided solution, and links to an
Overview page of formulas and to The Physics Classroom Tutorial pages. The Extra Problems pertain to various aspects of the topic of waves, wave mathematics, standing waves, etc..
Problem 1:
A cork resting on the surface of a pond bobs up and down 3 times per second on some ripples having a wavelength of 12.7 cm. If the cork is 16.7 m from shore, how long (in seconds) does it take a ripple passing the cork to reach the shore?
View Audio-Guided Solution.
Problem 2:
When a particular wire is vibrating with a frequency of 8.1 Hz, a transverse wave of wavelength 54.8 cm is produced. Determine the speed (in m/s) of the wave pulses along the wire.
Problem 3:
A particular piano emits frequencies that range from a low of about 37 Hz to a high of about 4335 Hz. Find the lowest wavelength wave (in centimeters). The speed of sound in air is approximately 343 m/s.
Problem 4:
(Referring to the previous problem.) Find the highest wavelength wave (in meters) produced by the piano.
Problem 5:
A harmonic wave is traveling along a rope. It is observed that the oscillator that generates the wave completes 46 vibrations in 53.5 s. Also, any given crest travels 601 cm along the rope in 10 s. What is the wavelength (in centimeters)?
Problem 6:
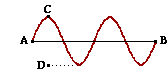A wave with a frequency of 17.3 Hz is traveling in the positive x direction as pictured in the diagram at the right. The horizontal distance from point A to point B is 37.5 cm. The vertical distance from point C to point D is 17.7 cm. Find the amplitude (in centimeters) of the wave.
Problem 7:
(Referring to the previous problem and diagram.) Find the wavelength (in centimeters) of the wave.
Problem 8:
(Referring to the previous problems and diagram.) Find the period (in milliseconds) of the wave.
Problem 9:
(Referring to the previous problems and diagram.) Find the speed (in centimeters/second) of the wave.
Problem 10:
For a certain transverse wave, it is observed that the distance between the two successive crests is 2.92 m. It is also noted that 10 crests pass a given point along the direction of travel every 18.3 seconds. Calculate the wave speed (in centimeters/second).
Problem 11:
How much time (in minutes) does it take light to reach us from the Sun, 93,000,000 mi away? (The speed of light is equal to 3.00 x 108 m/s; 1609 m = 1 mile.)
Problem 12:
A sound wave, traveling at 343 m/s, is emitted by the foghorn of a tugboat. An echo is heard 2.87 s later. How far away (in meters) is the reflecting object?
Problem 13:
Two boats - Boat A and Boat B - are anchored a distance of 25 meters apart. The incoming water waves force the boats to oscillate up and down, making one complete cycle every 14.2 seconds. When Boat A is at its peak, Boat B is at its low point and there is one wave crest between the two boats. The vertical distance between Boat A and Boat B at their extremes is 10.2 meters. Determine the speed (in meters/second) of the waves.
Problem 14:
(Referring to the previous problem.) Determine the amplitude (in meters) of the waves.
Problem 15:
A wave having a wavelength of 1.338 meters and an amplitude of 1.83 meters travels a distance of 74.5 meters in 4.67 seconds. Determine the frequency (in Hertz) of the waves.
Problem 16:
In a physics lab, a rope is observed to make 240 complete vibrational cycles in 15 seconds. The length of the rope is 2.7 meters and the measurements are made for the 6th harmonic. Determine the wavelength (in centimeters) of the waves.
Problem 17:
(Referring to the previous problem.) Determine the speed (in meters/second) of the waves in the rope.
Problem 18:
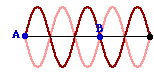A snakey vibrates in the manner shown in the diagram at the right. The distance from point A to point B is known to be 4.69 meters. When not being shook, a single pulse introduced into the medium at point A will travel to the opposite end and back in 2.7 seconds. Determine the vibrational frequency (in Hertz) of the wave pattern shown in the diagram. Enter your answer accurate to the third decimal place.
Problem 19:
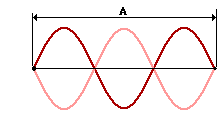A rope is held tightly and shook until the wave pattern shown in the diagram at the right is established within the rope. The distance A in the diagram is 3.27 meters. The speed at which waves move along the rope is 24.4 m/s. Determine the number of vibrational cycles occuring in 18.7 seconds.
Problem 20:
A 4.69-meter long rope undergoes 64 complete vibrational cycles in 17.6 seconds when vibrating in the third harmonic. Determine the speed (in meters/second) of the waves in the rope.