Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
 The previous part of Lesson 2 focused on the Law of Conservation of Momentum. It was stated that ...
The previous part of Lesson 2 focused on the Law of Conservation of Momentum. It was stated that ...
For a collision occurring between object 1 and object 2 in an isolated system, the total momentum of the two objects before the collision is equal to the total momentum of the two objects after the collision. That is, the momentum lost by object 1 is equal to the momentum gained by object 2.
Total system momentum is conserved for collisions occurring in isolated systems. But what makes a system of objects an isolated system? And is momentum conserved if the system is not isolated? This is the focus of this part of Lesson 2.
What is an Isolated System?
A system is a collection of two or more objects. An isolated system is a system that is free from the 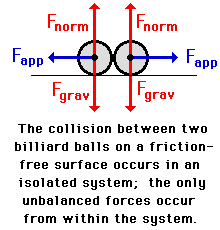 influence of a net external force that alters the momentum of the system. There are two criteria for the presence of a net external force; it must be...
influence of a net external force that alters the momentum of the system. There are two criteria for the presence of a net external force; it must be...
- a force that originates from a source other than the two objects of the system
- a force that is not balanced by other forces.
A system in which the only forces that contribute to the momentum change of an individual object are the forces acting between the objects themselves can be considered an isolated system.
Consider the collision of two balls on the billiards table. The collision occurs in an isolated system as long as friction is small enough that its influence upon the momentum of the billiard balls can be neglected. If so, then the only unbalanced forces acting upon the two balls are the contact forces that they apply to one another. These two forces are considered internal forces since they result from a source within the system - that source being the contact of the two balls. For such a collision, total system momentum is conserved.
 Read the following descriptions of a collision and evaluate whether or not the collision occurs in an isolated system. If it is not an isolated system, then identify the net external force.
Read the following descriptions of a collision and evaluate whether or not the collision occurs in an isolated system. If it is not an isolated system, then identify the net external force.
| |
Collision
Description
|
Isolated System?
Yes or No
|
If No, then the
external force is...
|
|
1.
|
Two cars collide on a gravel roadway on which frictional forces are large.
|
|
|
|
2.
|
Hans Full is doing the annual vacuuming. Hans is pushing the Hoover vacuum cleaner across the living room carpet.
|
|
|
|
3.
|
Two air track gliders collide on a friction-free air track.
|
|
|
The Money Transfer Analogy
If a system is not isolated, then the total system momentum is not conserved. To understand this concept, we will return to our original analogy. Suppose Jack and Jill (each with $100 in their pockets) undergo a financial interaction in which Jack hands Jill $50 for the purchase of some goods. If Jack and Jill were isolated from the influence of the rest of the world, then Jack would end up with $50 and Jill would end up with $150. The total money in the system would be $200 both before and after the transaction; total system money would be conserved. If however, a third influence enters from outside of the system to take away or (more fortunately) to add money to the system, then total system momentum would not be conserved. If a thief interfered with his filthy hands so as to steal $20, then perhaps Jack would finish with $40 and Jill would finish with $140. In the case of a non-isolated system, the total system momentum is not conserved.
Because of the inevitability of friction and air resistance in any real collision, one can conclude that no system is ever perfectly isolated. The reasoning is that there will always be a resistance force of some kind robbing the system of its momentum. For this reason, the law of conservation of momentum must be some sort of pie-in-the-sky idea that never has any applicability. Why does one ever need to learn a law that is always broken?
We friends of physics would quickly agree that resistance forces such as friction and air resistance are inevitable. However, one must be careful of overrating the impact of such forces on total system momentum. To illustrate, consider the collision between two 1000-kg cars - one that is initially at rest and one that is moving at 10 m/s (approximately 22 mi/hr). Such a collision would last for a fraction of a second. Suppose the actual contact forces between cars occur for 0.01 seconds. Perhaps after this very short 0.01 seconds, the cars stick together and slide a short distance across the asphalt street. For such a realistic collision, a typical contact force might be close to 500 000 N. A typical friction force would be no larger than 10 000 N (and would probably be considerably less). Each force would deliver an impulse to the vehicles during the collision in order to change the momentum of the colliding vehicles. The 500 000 N contact force between vehicles is an internal force and does not serve to change the momentum of the system. The 10 000 N friction force is an external force and would alter the total system momentum by approximately 200 kg•m/s (100 kg•m/s for each car). This loss of system momentum must be compared to the total system momentum of 10 000 kg•m/s. In this very realistic case, friction would cause no more than a 2% loss of total system momentum. If the collision being analyzed involved objects with even greater speeds, the percent loss of total system momentum would be considerably less.
So one must again consider the charge that the law of conservation of momentum is a pie-in-the-sky idea. The best response is to say that it is a very accurate model approximating the exchange of momentum between colliding objects. In the collision just described, the worse case scenario is that the assumption of momentum conservation is 98% accurate. Because contact forces during collisions are so large compared to the inevitable resistance forces such as friction and air resistance, the law of momentum conservation is a great tool for analyzing collisions and providing an accurate estimate of a post-collision (or a pre-collision) speed. In the next part of Lesson 2, the power of this conservation model to predict pre- and post-collision speeds of colliding objects will be illustrated.
We Would Like to Suggest ...

Sometimes it isn't enough to just read about it. You have to interact with it! And that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Cart and Brick Interactive,
Exploding Carts Interactive, and/or our
Collision Carts Ineractive. These Interactives can be found in the Physics Interactive section of our website and provide an interactive experience in analyzing the momentum of individual objects and systems of objects in collisions.