Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Lesson 3: Colligative Properties
Part c: Freezing Point Depression
Part a:
Vapor Pressure Lowering
Part b:
Boiling Point Elevation
Part c: Freezing Point Depression
What is Freezing Point Depression?
Lesson 3 has been highlighting a collection of properties of solutions that are known as colligative properties. Colligative properties are properties that are independent of the identity of the solute and dependent upon the number of particles of solute in the solution. Vapor pressure lowering was discussed in Lesson 3a and boiling point elevation was discussed in Lesson 3b.
In Lesson 3c, we will be discussing a third colligative property known as freezing point depression. Adding solute to a solvent like water causes the freezing point of the resulting solution to be less than that of the pure solvent. And the more particles of solute that are in the solution, the more that the freezing point will be decreased below that of the pure solvent. While the normal freezing point of pure water is 0°C, adding a solute like NaCl will cause the solution to freeze at a temperature below 0°C. The more solute that is added, the lower the freezing point will be dropped. This is known as freezing point depression.
If you live in a climate that is known for its winter snowstorms, then you may be familiar with the practice of salting roads and sidewalks. Rock salt (sodium chloride crystals) is scattered about road surfaces. The ionic solute dissolves in the wet snow and lowers the melting point of water. This reduces the likelihood of the precipitation freezing as temperatures drop and prevents the formation of dangerous icy road conditions. Though more expensive, calcium chloride crystals are often used on residential sidewalks for even greater protection from freezing surfaces. These are great examples of Chemistry for Better Living (at least until you have to replace your rusted tailpipe on your automobile the following spring).
Explaining Freezing Point Depression
Freezing involves the change of a substance from the liquid to the solid state. The distinction between these two states of matter was discussed in Chapter 11 of our Chemistry Tutorial. The solid state is a lower-energy state characterized by strong intermolecular forces and highly organized arrangements of particles. When an aqueous solution begins to freeze, the water molecules must transition from its role as solvator of solute particles and re-arrange themselves into a cystalline structure. The process is an endothermic process in which energy is removed from the solution The presence of the solute partcles makes it more difficult for the water to organize itself and requires even more removal of energy. As such, even lower temperatures are required for the water molecules to re-organize into a solid structure.
It is interesting to note that it is the solvent that is freezing and not the solution. For instance, it is the water of an aqueous solution that undergoes the freezing. Water is doing the re-organizing into a pure crystal lattice. The dissolved solute particles remain left behind in the unfrozen portion of the solution. Since the amount of solvent is reduced by the freezing process, the solution becomes more concentrated with solute particles. This in turn lowers the freezing point even more.
Dependence on the Number of Particles
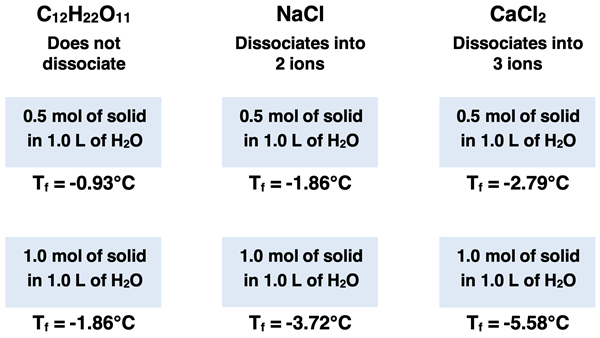
Like all colligative properties, the amount that the freezing point of a solution is lowered is dependent upon the number of solute particles dissolved in the solution. Higher concentrations of solutes result in a greater depression of the freezing point. And ionic solutes that dissociate into ions will have a greater effect upon the freezing point than molecular solids that do not dissociated. Finally, an ionic solid that dissociates into three ions (e.g., CaCl2) will reduce the freezing point more than an ionic solute that dissociates into two ions (for example, NaCl). These are the same patterns that were observed for vapor pressure lowering and boiling point elevation.
To illustrate the importance of dissolved solute particles, suppose that 0.500 mole and 1.00 mole of varying solids were added and stirred into 1.00 L of water. The freezing point depression would vary depending upon how much solid was dissolved in the water and on how many ions the solid dissociates into.
Freezing Point Depression Equation
As you might expect, there is an equation for predicting how much the freezing point of a solution is lowered by the presence of dissolved solute particles. The equation for the freezing point depression (∆Tf) is
∆Tf = i • Kb • molality
The ∆Tf is the difference between the freezing point of the solution (Tf-solution) and the freezing point of the pure solvent (Tf-pure solvent).
∆Tf = Tf-solution - Tf-pure solvent
The Kf in the equation is referred to as the freezing point depression constant. It is a value that depends upon the solvent. A table of values for several common solvents is shown at the right. The negative values are consistent with the fact that the freezing point change is a negative change; that is, it decreases with the addition of solute.
The i in the equation is known as the Van’t Hoff factor. For molecular solids that don’t dissociate, the value is 1. For ionic solids like NaCl that dissociate into two ions, the value is 2. For ionic solids like CaCl2 that dissociate into three ions, the value is 3.
The molality is a concentration unit. It is defined as the moles of solute per kilogram of solvent.
Example 1
An aqueous solution is prepared by dissolving 10.00 grams of copper(II) chloride in 200.0 mL of water. Predict the freezing point depression of the solution.
Solution:
The plan will involve using ∆Tf = I • Kf • molality to determine the decrease in freezing point temperature.
As a first step, we will determine the molality of the solution. We will calculate the moles of solute from the mass of solute. We will calculate the mass of solvent from the volume.
Moles solute = 10.00 g CuCl2 • (1 mol CuCl2 / 135.45 g CuCl2)
Moles solute = 0.07382798 … mol CuCl2
Mass of solute = 0.2000 L • (1.00 kg/L) = 0.200 kg
Molality = (0.07382798 … mol CuCl2) / (0.200 kg) = 0.3691399 … mol/kg
As a second step, we will calculate the freezing point depression using the K
f of water - -1.86°C•kg/mol. The value of i in the equation is 3 since CuCl
2 dissociates into three ions.
∆Tf = i•Kb•molality = 3•(-1.86°C•kg/mol) • (0.3691399 … mol/kg)
∆Tf = -2.059800 … °C
The freezing point of the solution is
-2.06°C.
Before You Leave
- Download our Study Card on Colligative Properties. Save it to a safe location and use it as a review tool. (Coming Soon.)
- The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.
Check Your Understanding
Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
1. Rank the following samples in order of increasing freezing point, from lowest to highest.
- Sample A: Pure Water
- Sample B: 0.25 M C12H22O11(aq)
- Sample C: 0.25 M KCl(aq)
2. Rank the following samples in order of increasing freezing point, from lowest to highest.
- Sample A: 0.50 M NaCl(aq)
- Sample B: 1.50 M NaCl(aq)
- Sample C: 0.10 M NaF(aq)
3. Rank the following samples in order of increasing freezing point, from lowest to highest.
- Sample A: 1.00 M KCl(aq)
- Sample B: 1.00 M CuCl2(aq)
- Sample C: 1.00 M AlCl3(aq)
View:
Chapter Contents