Vectors and Projectiles: Extra Problems
The problems below are provided as additional problems to
the original set of 34 Vector and Projectiles problems. Just like problems in the original set, these problems consist of a problem, an answer (revealed by clicking a link), an audio guided solution, and links to an
Overview page of formulas and to The Physics Classroom Tutorial pages. The Extra Problems pertain to various aspects of the topic of vectors, vector addition, vector resolution, vector components, relative velocity, and projectile motion. The problems are divided into four separate sets of problems. The first two sets pertain to vectors and their operations. The last two sets pertain to projectile motion.
Problem Set A
Problem 1:
A man lost in a maze makes three consecutive displacements such that at the end of the walk he is right back where he started. The first displacement is 9.3 m westward, and the second is 10.8 m northward. Find the magnitude (in meters) of the third displacement.
View Audio Solution.
Problem 2:
(Referring to the previous problem.) Find the direction (in degrees) of the third displacement. (Use the counter-clockwise from east convention.)
Problem 3:
A quarterback takes the ball from the line of scrimmage, runs backward for 8.5 yards, then sideways parallel to the line of scrimmage for 10.8 yards. At this point, he throws a 37.1-yard forward pass straight down field perpendicular to the line of scrimmage. What is the magnitude (in yards) of the football's resultant displacement?
Problem 4:
A shopper pushing a cart through a store moves a distance 30.0 m down one aisle then makes a 90 degree turn to his right and moves 11.8 m. He then makes another 90 degree turn to his left and moves 16.8 m. How far (in meters) is the shopper away from his original position?
Problem 5:
(Referring to the previous problem.) What is the direction (in degrees) of the shopper's displacement (relative to the original line of motion)? (Enter a positive value.)
Problem 6:
What is the magnitude of the resultant displacement (in meters) of a walk of 61.7 m followed by a walk of 88.0 m when both displacements are in the eastward direction?
Problem 7:
What is the magnitude of the resultant displacement (in meters) in a situation in which the 88.0 m walk is in the direction opposite the 61.7 m walk?
Problem 8:
At the beginning of a roller coaster ride, a coaster car moves 138 ft horizontally, then rises 102 ft at an angle of 24.0 degree above the horizontal. It then travels 102 ft at an angle of 29.5 degree downward below the horizontal. What is its displacement (in feet) from its starting point at the end of this movement?
Problem 9:
A dog searching for a bone walks 4.98 m south, then 9.01 m at an angle 30.0 degree north of east, and finally 13.01 m west. Find the dog's resultant displacement (in meters).
Problem 10:
A jogger runs 88 m due west, then changes direction for the second leg of the run. At the end of the run, she is 107 m away from the starting point at an angle of 22.5 degree north of west. What was the length (in meters) of her second displacement?
Problem 11:
(Referring to the previous problem.) What was the direction (in degrees) of the second displacement? (Use the counter-clockwise from east convention.)
Problem 12:
A roller coaster travels 109 ft at an angle of 23.5 degree above the horizontal. How far (in feet) does it move horizontally?
Problem 13:
(Referring to the previous problem.) How far (in feet) does it move vertically?
Problem 14:
A submarine dives at an angle of 20.9 degrees with the horizontal and follows a straight-line path for a total distance of 176 m. How far (in meters) is the submarine below the surface of the water?
Problem 15:
During the Vector Addition lab, Mac and Tosh start at the classroom door and walk 10.2 m, north, 17.5 m west, 16.4 m south, 11.7 m west, and 5.5 m, north. Determine the magnitude of the resulting displacement (in meters) of Mac and Tosh.
Problem Set B
Problem 1:
The two displacement vectors A and B have a magnitude of 2.98 m. Vector A has a direction of 108 degrees. Vector B has a direction of 211 degrees. Find the magnitude (in meters) of A + B using component analysis.
Problem 2:
(Referring to the previous problem.) Use component analysis to determine the magnitude (in meters) of A - B.
View Audio Solution.
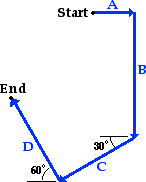
Problem 3:
A person going for a walk follows the path shown in the unscaled diagram at the right. The total trip consists of four straight- line paths. The magnitude of the individual displacements are: A = 88 m; B = 272 m; C = 136 m; D = 183 m. At the end of the walk, what is the person's resultant displacement (in meters) measured from the starting point?
View Audio Solution.
Problem 4:
An airplane flies from city A to B in a direction due east for 732 miles. In the next part of the trip the airplane flies from city B to city C in a direction 35.5 degrees north of east for 514 miles. What is the magnitude (in miles) of the resultant displacement of the airplane between city A and city C?
View Audio Solution.
Problem 5:
(Referring to the previous problem.) What is the direction (in degrees) of the resultant displacement of the airplane? Use the counter-clockwise from east convention.
View Audio Solution.
Problem 6:
While exploring a cave, a spelunker starts at the entrance and moves the following distances. She goes 68 m north, 246 m east, 112 m at an angle 30 degrees north of east, and 159 m south. Find the magnitude of the resultant displacement (in meters) from the cave entrance.
View Audio Solution.
Problem 7:
(Referring to the previous problem.) What is the direction (in degrees) of the resultant displacement? Use the counter-clockwise from east convention.
View Audio Solution.
Problem #8
An airplane begins its journey into Canada from a destination located 285 mi south of the border. The plane flies along a straight-line path at 189 mi/h in a direction of 20.5 degrees west of north. Determine the number of minutes before the plane crosses the border.
View Audio Solution.
Problem 9:
An escalator is 18.5 m long. If a person stands on the 'up' side, it takes 50.9 s to ride to the top. If a person walks up the moving escalator with a speed of 0.505 m/s relative to the escalator, how long (in seconds) does it take to the get to the top?
View Audio Solution.
Problem 10:
(Referring to the previous problem.) If a person walks down the 'up' escalator with the same relative speed as in the previous problem, how long (in seconds) does it take to reach the bottom.
View Audio Solution.
Problem 11:
A boat moves at 4.9 m/s relative to the water regardless of which direction it travels through the water. If the water in a river is flowing at 1.5 m/s, how long (in seconds) does it take the boat to make a round trip consisting of a 285 m displacement downstream followed by a 285 m displacement upstream.
View Audio Solution.
Problem 12:
A river flows due east at 2.5 m/s. A boat crosses the river from the south shore to the north shore by maintaining a constant velocity of 7.3 m/s due north relative to shore. What is the magnitude of the velocity of the boat (in m/s) relative to the shore?
View Audio Solution.
Problem 13:
(Referring to the previous problem.) If the river is 242 m wide and the boat heads directly across it, then how much time (in seconds) does it take the boat to reach the opposite shore?
View Audio Solution.
Problem 14:
(Referring to the previous problem.) If the river is 242 m wide and the boat heads directly across it, then how far downstream (in meters) has the boat moved by the time it reaches the North shore?
View Audio Solution.
Problem 15:
The pilot of an aircraft wishes to fly due west in a wind blowing at 45 km/h toward the south. If the speed of the aircraft in the absence of wind is 165 km/h, in what direction (in degrees) should the aircraft head? Use the counter-clockwise from east convention.
View Audio Solution.
Problem 16:
(Referring to the previous problem.) What will be the airplane's speed (in km/h) relative to the ground?
View Audio Solution.
Problem 17:
Two canoeists in identical canoes exert the same effort paddling and hence maintain the same speed relative to the water. One paddles directly upstream (and moves upstream), whereas the other paddles directly downstream. Downstream is the positive direction. An observer on shore determines the velocities of the two canoes to be -1.02 m/s and +2.56 m/s respectively. What is the speed of the water (in m/s) relative to shore?
View Audio Solution.
Problem 18:
A boat heads due east directly across a 117-m wide river. The water flows due south with a speed of 2.1 m/s with respect to the shore. The boat speed with respect to the water is 2.9 m/s. Determine the magnitude of the velocity (in m/s) with respect to the shore.
View Audio Solution.
Problem 19:
(Referring to the previous problem.) Determine the direction (in degrees) of the velocity with respect to the shore. Use the counter-clockwise from east convention.
View Audio Solution.
Problem 20:
(Referring to the previous problem.) Determine the distance (in m) that the boat will have traveled downstream when it has reached the opposite shore.
View Audio Solution.
Problem Set C
Problem 1:
A stone is dropped from rest off the top of a 89.2-m high cliff. How much time (in seconds) does it take the stone to reach the ground below?
View Audio Solution.
Problem 2:
A stone is thrown with an initial horizontal velocity of 8.48 m/s off the top of a 89.2 m high cliff. How much time (in seconds) does it take the stone to reach the ground below?
View Audio Solution.
Problem 3:
(Referring to the previous problem.) How far (in meters) from the base of the cliff does the stone land?
View Audio Solution.
Problem 4:
Tom the cat is chasing Jerry the mouse across a table surface 1.58 m high. Jerry steps out of the way at the last second, and Tom slides off the edge of the table at a speed of 6.89 m/s. How many meters from the bottom edge of the table will Tom strike the floor?
View Audio Solution.
Problem 5:
(Referring to the previous problem.) What is the horizontal component of velocity (in m/s) of the cat just prior to hitting the floor?
View Audio Solution.
Problem 6:
(Referring to the previous problem.) What is the vertical component of velocity (in m/s) of the cat just prior to hitting the floor?
View Audio Solution.
Problem 7:
A watermelon is rolled off a high-diving platform with an initial speed of 3.94 m/s. The melon lands in the water 3.97 s later. Determine the height (in meters) of the diving platform.
View Audio Solution.
Problem 8:
(Referring to the previous problem.) How far (in meters) from the base of the platform does the watermelon land?
View Audio Solution.
Problem 9:
What is the speed (in m/s) of the watermelon the instant before it strikes the water?
View Audio Solution.
Problem 10:
The Aculpulco cliff divers dive from a cliff that is 64.7 m high. The rocks below the cliff extend horizontally outward for 27.7 m. What is the minimum horizontal velocity (in m/s) a diver must have when leaving the cliffs to clear the rocks safely? Assume that the divers take a horizontal leap off the cliff.
View Audio Solution.
Problem 11:
Two objects are initially the same height above the ground. Simultaneously, one is released from rest and the other is shot off horizontally with an initial speed of 3.45 m/s. The two objects collide after falling 26.6 m. How far apart (in meters) were the objects initially?
View Audio Solution.
Problem 12:
A ball rolls off a 148-cm high table and hits the ground a distance of 2.96 m from the base of the table. Determine the speed (in m/s) of the ball the moment it leaves the table.
View Audio Solution.
Problem 13:
(Referring to the previous problem.) Determine the magnitude of the acceleration (in m/s/s) of the ball after it has fallen halfway to the ground.
View Audio Solution.
Problem 14:
(Referring to the previous problem.) Determine the speed (in m/s) of the ball just prior to hitting the ground.
View Audio Solution.
Problem 15:
A Hot Wheels car rolls off a table at a speed of 3.45 m/s and hits the floor a distance of 118.8 cm from the table's edge. Determine the height (in cm) of the table.
View Audio Solution.
Problem 16:
An airplane is traveling 1188 meters above the ocean at a speed of 182 km/hr. The plane wishes to drop a box of supplies to shipwrecked victims in the water below. In order to have a successful mission, how far horizontally (in meters) from the wreckage site must the plane be when dropping the package?
View Audio Solution.
Problem 17:
A student throws a baseball horizontally out a dorm room window 29.6 m above the ground. Another student standing a distance of 34.6 m from the dorm building catches the baseball at a height of 1.6 m above the ground. What is the initial velocity (in m/s) of the baseball?
View Audio Solution.
Problem 18:
A projectile is launched from the ground with a velocity of 69.1 m/s, directed at a angle of 64.4 degrees with the horizontal. Resolve this velocity vector into horizontal and vertical components. Then determine the time (in seconds) that the projectile is in the air before landing.
View Audio Solution.
Problem 19:
(Referring to the previous problem.) Determine the horizontal displacement (in meters) of the projectile.
View Audio Solution.
Problem 20:
(Referring to the previous problem.) Determine the maximum vertical height (in meters) of the projectile - achieved when at the midpoint of its trajectory.
View Audio Solution.
Problem Set D
Problem 1:
A punter kicks a football at an angle of 28.6 degrees with the horizontal at an initial speed of 20.9 m/s. What distance (in meters) away should a punt returner position himself to catch the ball just before it strikes the ground?
View Audio Solution.
Problem 2:
(Referring to the previous problem.) To what vertical height (in meters) does the football rise above the initial location?
View Audio Solution.
Problem 3:
A tennis player stretches out to reach a ball that is just barely above the ground and successfully 'lobs' it over her opponent's head. The ball is hit with a speed of 19.7 m/s at an angle of 65.1 degrees. Determine the time (in seconds) that the ball is in the air.
View Audio Solution.
Problem 4:
(Referring to the previous problem.) Determine the height (in meters) to which the ball rises above the court.
View Audio Solution.
Problem 5:
(Referring to the previous problem.) Determine how far away (in meters) the ball lands relative to its striking location.
View Audio Solution.
Problem 6:
A brick is thrown upward from the top of a building at an angle of 22.9 degrees to the horizontal and with an initial speed of 11.7 m/s. If the brick is in flight for 2.67 s, how tall (in meters) is the building?
View Audio Solution.
Problem 7:
(Referring to the previous problem.) How far away (in meters) from the base of the building will the brick land?
View Audio Solution.
Problem 8:
In an ideal punt, the football has a 'hangtime' (total time in the air) of 4.70 s. If a punter kicks the ball at an angle of 39.9 degrees with the horizontal, what must be the initial velocity (in m/s) of the ball to achieve this?
View Audio Solution.
Problem 9:
(Referring to the previous problem.) To what height (in meters) will such a punt rise above the ground?
View Audio Solution.
Problem 10:
A daredevil is shot out of a cannon at 41.7 degrees to the horizontal with an initial speed of 25.1 m/s. A net is located a horizontal distance of 48.6 m from the cannon. At what height (in meters) above the cannon should the net be placed in order to catch the daredevil?
View Audio Solution.
Problem 11:
A ball is thrown straight upward and returns to the thrower's hand after 3 s in the air. A second ball is thrown at an angle of 28.6 degrees with the horizontal. At what speed (in m/s) must the second ball be thrown so that it reaches the same height as the one thrown vertically?
View Audio Solution.
Problem 12:
A pitcher throws a ball horizontally with a speed of 134 km/hr from a height of 1.57 meters above the field. Home plate is a distance of 18.4 meters away. The batter's combined reaction and swing time is .324 seconds. How much time (in milliseconds) can the batter watch the ball after it has left the pitcher's hand before making a decision to swing?
View Audio Solution.
Problem 13:
A ditch 2.34 m wide crosses a trailbike path. An upward incline of 15.1 degrees has been built up on the approach so that the top of the incline is level with the top of the ditch. What is the minimum speed (in m/s) at which a trailbike must be moving to completely clear the ditch? (Add 1.2 m to the range for the back of the bike to clear the ditch safely.)
View Audio Solution.
Problem 14:
A mountain climber is stranded on a ledge 139 m above the ground. Rescuers on the ground want to shoot a projectile to him with a rope tied to it. If the projectile is directed upward at an initial angle of 58 degrees and fired at the ledge from a horizontal distance of 109 m, determine the initial speed (in m/s) the projectile must have to hit the ledge.
View Audio Solution.
Problem 15:
A car is parked on a cliff overlooking the ocean on an incline that makes an angle of 26.2 degrees below the horizontal. The negligent driver leaves the car in neutral, and the emergency brakes are defective. The car rolls from rest down the incline with a constant acceleration of 4.20 m/s/s and travels 48.6 m to the edge of the cliff. The cliff is 33.6 m above the ocean. Find the speed (in m/s) of the car the moment it leaves the cliff.
View Audio Solution.
Problem 16:
(Referring to the previous problem.) Find the time (in seconds) it takes the car to drop to the ocean below the edge of the cliff.
View Audio Solution.
Problem 17:
(Referring to the previous problem.) Find the position (in meters) of the car relative to the base of the cliff when it lands in the ocean.
View Audio Solution.
Problem 18:
A firefighter holds a hose which emits water with a velocity of 22.1 m/s at an angle of 54.9 degrees above the horizontal. He stands a horizontal distance of 22.9 m from a building with the intent of projecting the water to a high window. What height (in meters) on the building will the water reach?
View Audio Solution.
Problem 19:
A daredevil decides to jump a canyon of width 11.9 m. To do so, he drives a motorcycle up an incline sloped at an angle of 14.4 degrees. What minimum speed (in m/s) must he have in order to clear the canyon? (Assume that the initial and final heights are the same.)
View Audio Solution.
Problem 20:
(Referring to the previous problem.) To what maximum height (in meters) above the top of the ramp will the daredevil ascend?
View Audio Solution.