Which Path Requires the Most Energy?
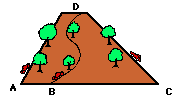 Suppose that a car traveled up three different roadways (each with varying incline angle or slope) from the base of a mountain to the summit of the mountain. Which path would require the most gasoline (or energy)? Would the steepest path (path AD) require the most gasoline or would the least steep path (path BD) require the most gasoline? Or would each path require the same amount of gasoline?
Suppose that a car traveled up three different roadways (each with varying incline angle or slope) from the base of a mountain to the summit of the mountain. Which path would require the most gasoline (or energy)? Would the steepest path (path AD) require the most gasoline or would the least steep path (path BD) require the most gasoline? Or would each path require the same amount of gasoline?
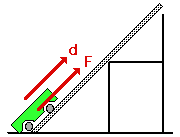 This situation can be simulated by use of a simple physics lab in which a force is applied to raise a cart up an incline at constant speed to the top of a seat. Three different incline angles could be used to represent the three different paths up the mountain. The seat top represents the summit of the mountain. And the amount of gasoline (or energy) required to ascend from the base of the mountain to the summit of the mountain would be represented by the amount of work done on the cart to raise it from the floor to the seat top. The amount of work done to raise the cart from the floor to the seat top is dependent upon the force applied to the cart and the displacement caused by this force. Typical results of such a physics lab are depicted in the animation below.
This situation can be simulated by use of a simple physics lab in which a force is applied to raise a cart up an incline at constant speed to the top of a seat. Three different incline angles could be used to represent the three different paths up the mountain. The seat top represents the summit of the mountain. And the amount of gasoline (or energy) required to ascend from the base of the mountain to the summit of the mountain would be represented by the amount of work done on the cart to raise it from the floor to the seat top. The amount of work done to raise the cart from the floor to the seat top is dependent upon the force applied to the cart and the displacement caused by this force. Typical results of such a physics lab are depicted in the animation below.
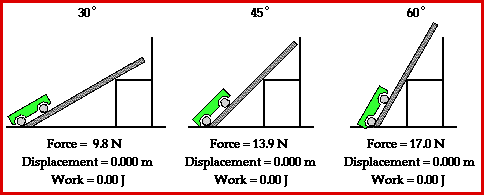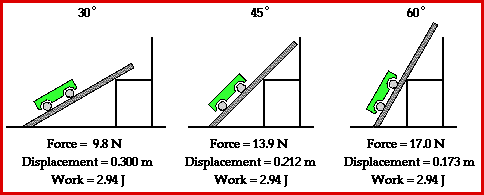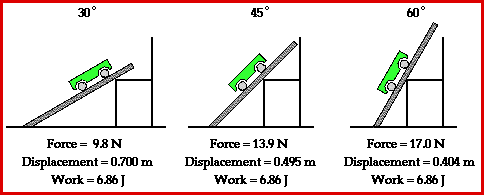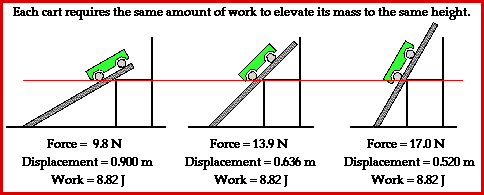
Observe in the animation that each path up to the seat top (representing the summit of the mountain) requires the same amount of work. The amount of work done by a force on any object is given by the equation
Work = F * d * cosine(Theta)
where F is the force, d is the displacement and Theta is the angle between the force and the displacement vector.
The least steep incline (30-degree incline angle) will require the least amount of force while the most steep incline will require the greatest amount of force. Yet, force is not the only variable affecting the amount of work done by the car in ascending to a certain elevation. Another variable is the displacement which is caused by this force. A look at the animation above reveals that the least steep incline would correspond to the largest displacement and the most steep incline would correspond to the smallest displacement. The final variable is Theta - the angle between the force and the displacement vector. Theta is 0-degrees in each situation. That is, the force is in the same direction as the displacement and thus makes a 0-degree angle with the displacement vector. So when the force is greatest (steep incline) the displacement is smallest and when the force is smallest (least steep incline) the displacement is largest. Subsequently, each path happens to require the same amount of work to elevate the object from the base to the same summit elevation.
Another perspective from which to analyze this situation is from the perspective of potential and kinetic energy and work. The work done by an external force (in this case, the force applied to the cart) changes the total mechanical energy of the object. In fact, the amount of work done by the applied force is equal to the total mechanical energy change of the object. The mechanical energy of the cart takes on two forms - kinetic energy and potential energy. In this situation, the cart was pulled at a constant speed from a low height to a high height. Since the speed was constant, the kinetic energy of the cart was not changed. Only the potential energy of the cart was changed. In each instance (30-degree, 45-degree, and 60-degree incline), the potential energy change of the cart was the same. The same cart was elevated from the same initial height to the same final height. If the potential energy change of each cart is the same, then the total mechanical energy change is the same for each cart. Finally, it can be reasoned that the work done on the cart must be the same for each path.
For more information on physical descriptions of motion, visit The Physics Classroom Tutorial. Detailed information is available there on the following topics:
Work
Forces on Inclined Planes
Potential Energy
Kinetic Energy
Mechanical Energy
Internal vs. External Forces
Work-Energy Theorem