|
Three resistors are connected in series. If placed in a circuit with a 120-Volt power supply. Determine the equivalent resistance, the total circuit current, and the voltage drop across and current through each resistor. Enter your answers to the third decimal place.
|
|
|
Often times, success in physics demands that you have the proper approach - a good game plan. The following strategy should serve you well:
-
Determine the equivalent resistance of the entire circuit. See Formula Fix section below.
-
Determine the current in the battery using the equivalent resistance and the battery voltage. See first Physics Rules section below.
-
Since current is the same in each resistor of a series circuit, you can quickly determine the values of I1, I2 and I3.
-
Use the current and the resistance of each resistor to determine the voltage drop across each individual resistor. See second Physics Rules section below.
-
As a final check, the sum of the voltage drops across each individual resistance should equal the battery voltage. While this check is not necessary, it is a wise habit to perform it in order to quickly catch any errors.
|
|
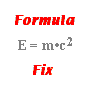
|
For series circuits, the mathematical formula for computing the equivalent resistance (Req) from the resistance values of the individual resistors (R1, R2, R3, ...) is
Req = R1 + R2 + R3 + ...
|
|

|
Current in a Series Circuit:
The overall current in a series circuit is no different than the current in an individual resistor. That is, the current through the battery is the same as the current in resistor 1 or resistor 2 or resistor 3 or ... . Since there are no branching locations, current is never divided and is everywhere the same. The amount of current is related to the voltage ( Vtot) impressed across the circuit by the battery and the overall equivalent resistance (Req). In equation form, these ideas can be written as Vtot) impressed across the circuit by the battery and the overall equivalent resistance (Req). In equation form, these ideas can be written as
Itot = I1 = I2 = I3 =  Vtot / Req Vtot / Req
|

|
Voltage Drops in a Series Circuit:
Charge gains energy (and electric potential) in the battery and loses energy (and electric potential) in the external circuit. The amount of electric potential gain in the battery is equal to the amount of loss in the external circuit. For series circuits, this loss occurs in a stepwise fashion as the charge passes through each resistor. The sum of the voltage drops across each resistor is equal to the voltage rating of the battery. The voltage drop across an individual resistor within a series circuit can be determined from the resistance of the resistor and the current through the circuit. For example:
 V1 = I • R1 V1 = I • R1  V2 = I • R2 V2 = I • R2  V3 = I • R3 V3 = I • R3
|
|
 What is an effective method of mathematically analyzing a series circuit? What is an effective method of mathematically analyzing a series circuit?
|