Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
The orbits of satellites about a central massive body can be described as either circular or elliptical. As mentioned earlier in Lesson 4, a satellite orbiting about the earth in circular motion is moving with a constant speed and remains at the same height above the surface of the earth. It accomplishes this feat by moving with a tangential velocity that allows it to fall at the same rate at which the earth curves. At all instances during its trajectory, the force of gravity acts in a direction perpendicular to the direction that the satellite is moving. Since perpendicular components of motion are independent of each other, the inward force cannot affect the magnitude of the tangential velocity. For this reason, there is no acceleration in the tangential direction and the satellite remains in circular motion at a constant speed. A satellite orbiting the earth in elliptical motion will experience a component of force in the same or the opposite direction as its motion. This force is capable of doing work upon the satellite. Thus, the force is capable of slowing down and speeding up the satellite. When the satellite moves away from the earth, there is a component of force in the opposite direction as its motion. During this portion of the satellite's trajectory, the force does negative work upon the satellite and slows it down. When the satellite moves towards the earth, there is a component of force in the same direction as its motion. During this portion of the satellite's trajectory, the force does positive work upon the satellite and speeds it up. Subsequently, the speed of a satellite in elliptical motion is constantly changing - increasing as it moves closer to the earth and decreasing as it moves further from the earth. These principles are depicted in the diagram below.

In Unit 5 of The Physics Classroom, motion was analyzed from an energy perspective. The governing principle that directed our analysis of motion was the work-energy relationship. Simply put, the theorem states that the initial amount of total mechanical energy (TMEi) of a system plus the work done by external forces (Wext) on that system is equal to the final amount of total mechanical energy (TMEf) of the system. The mechanical energy can be either in the form of potential energy (energy of position - usually vertical height) or kinetic energy (energy of motion). The work-energy theorem is expressed in equation form as
KEi + PEi + Wext = KEf + PEf
The Wext term in this equation is representative of the amount of work done by external forces. For satellites, the only force is gravity. Since gravity is considered an internal (conservative) force, the Wext term is zero. The equation can then be simplified to the following form.
KEi + PEi = KEf + PEf
In such a situation as this, we often say that the total mechanical energy of the system is conserved. That is, the sum of kinetic and potential energies is unchanging. While energy can be transformed from kinetic energy into potential energy, the total amount remains the same - mechanical energy is conserved. As a satellite orbits earth, its total mechanical energy remains the same. Whether in circular or elliptical motion, there are no external forces capable of altering its total energy.
|
Work and Energy Web Links
Perhaps at this time you would like to use the links below to review Unit 5 concepts at The Physics Classroom.
|
Energy Analysis of Circular Orbits
Let's consider the circular motion of a satellite first. When in circular motion, a satellite remains the same distance above the  surface of the earth; that is, its radius of orbit is fixed. Furthermore, its speed remains constant. The speed at positions A, B, C and D are the same. The heights above the earth's surface at A, B, C and D are also the same. Since kinetic energy is dependent upon the speed of an object, the amount of kinetic energy will be constant throughout the satellite's motion. And since potential energy is dependent upon the height of an object, the amount of potential energy will be constant throughout the satellite's motion. So if the KE and the PE remain constant, it is quite reasonable to believe that the TME remains constant.
surface of the earth; that is, its radius of orbit is fixed. Furthermore, its speed remains constant. The speed at positions A, B, C and D are the same. The heights above the earth's surface at A, B, C and D are also the same. Since kinetic energy is dependent upon the speed of an object, the amount of kinetic energy will be constant throughout the satellite's motion. And since potential energy is dependent upon the height of an object, the amount of potential energy will be constant throughout the satellite's motion. So if the KE and the PE remain constant, it is quite reasonable to believe that the TME remains constant.
One means of representing the amount and the type of energy possessed by an object is a work-energy bar chart. A work-energy bar chart represents the energy of an object by means of a vertical bar. The length of the bar is representative of the amount of energy present - a longer bar representing a greater amount of energy. In a work-energy bar chart, a bar is constructed for each form of energy. A work-energy bar chart is presented below for a satellite in uniform circular motion about the earth. Observe that the bar chart depicts that the potential and kinetic energy of the satellite are the same at all four labeled positions of its trajectory (the diagram above shows the trajectory).

Energy Analysis of Elliptical Orbits
Like the case of circular motion, the total amount of mechanical energy of a satellite in elliptical motion also remains constant. Since the only force doing work upon the satellite is an internal (conservative) force, the Wext term is zero and mechanical energy is conserved. Unlike the case of circular motion, the energy of a satellite in elliptical motion will change forms. As mentioned above, the force of gravity does work upon a satellite to slow it down as it moves away from the earth and to speed it up as it moves towards the earth. So if the speed is changing, the kinetic energy will also be changing. The elliptical trajectory of a satellite is shown below.
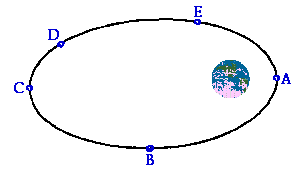
The speed of this satellite is greatest at location A (when the satellite is closest to the earth) and least at location C (when the satellite is furthest from the earth). So as the satellite moves from A to B to C, it loses kinetic energy and gains potential energy. The gain of potential energy as it moves from A to B to C is consistent with the fact that the satellite moves further from the surface of the earth. As the satellite moves from C to D to E and back to A, it gains speed and loses height; subsequently there is a gain of kinetic energy and a loss of potential energy. Yet throughout the entire elliptical trajectory, the total mechanical energy of the satellite remains constant. The work-energy bar chart below depicts these very principles.

An energy analysis of satellite motion yields the same conclusions as any analysis guided by Newton's laws of motion. A satellite orbiting in circular motion maintains a constant radius of orbit and therefore a constant speed and a constant height above the earth. A satellite orbiting in elliptical motion will speed up as its height (or distance from the earth) is decreasing and slow down as its height (or distance from the earth) is increasing. The same principles of motion that apply to objects on earth - Newton's laws and the work-energy theorem - also govern the motion of satellites in the heavens.
We Would Like to Suggest ...

Sometimes it isn't enough to just read about it. You have to interact with it! And that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Orbital Motion Interactive. You can find it in the Physics Interactives section of our website. The
Orbital Motion Interactive allows a learner to explore concepts and relationships associated with a satellite's orbital velocity, acceleration, and eccentricity of orbit in an interactive manner.