The Physics Classroom » Physics Tutorial » Balance and Rotation » Centripetal Angular and Tangential Acceleration
Balance and Rotation - Lesson 1 - Rotational Kinematics

Getting your Trinity Audio player ready...

Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.

Keeping Acceleration Straight

Previously in this lesson, we explored the concept of angular acceleration, the kind of acceleration that comes about as a rotating object increases or decreases its angular velocity.  A child standing on a rotating platform experiences an angular acceleration when the platform is pushed to speed it up or when friction causes it to slow down.  Earlier in this lesson, we also saw that a point on a rotating object that is experiencing an angular acceleration is also experiencing a tangential acceleration.  We call it a tangential acceleration since it points in a direction tangent to the circle.  For example, if the rotating platform with the child on it is speeding up, we would say that the child also has a tangential acceleration.

In Lesson 2 of Circular Motion and Satellite Motion, we also explored centripetal acceleration, the kind of acceleration experienced by any object moving in a circle.  When the child is rotating on the platform, she experiences a centripetal acceleration—whether she is speeding up, slowing down, or spinning at a constant speed. So, we have three kinds of acceleration?  We do.  How do we keep them straight?  That’s the purpose of this part of our lesson. 

Let’s consider a child on a rotating platform that is speeding up while spinning counterclockwise.  Here are a side view and a top view to help us ‘see’ these accelerations.

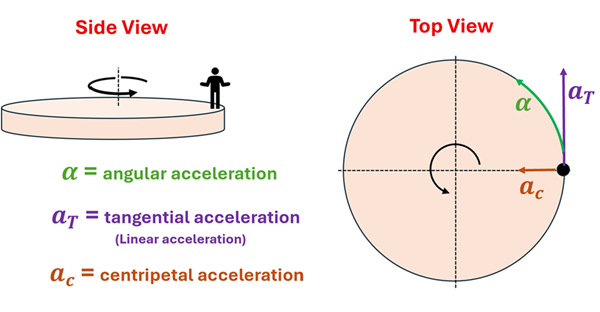
A side and top view of a rotating disc with arrows depicting the types of acceleration. A person is standing at the edge of the disc (at 0 degrees) and it is rotating counter clockwise. From the top view, a green arrow is arcing with the circle and labeled alpha (angular acceleration). An arrow straight up is labeled a sub t (tangential acceleration - linear), and a smaller arrow is pointing straight towards the center of the circle and is labeled a sub c (centripetal acceleration)

Earlier in this lesson, we saw that angular acceleration and tangential acceleration are related through one of our link equations (aT = r ⍺).  In a sense, they are describing the same speeding up (or slowing down) type of rotational motion.   However, the tangential acceleration depends on the child’s location on the platform, whereas his angular acceleration does not.  Centripetal acceleration, on the other hand, cannot be directly calculated from either of the other two types of accelerations.  This third type of acceleration points radially inward and has nothing to do with the fact that the platform is speeding up or slowing down but instead depends on the instantaneous speed of the child and how far he is from the center of the platform.  Let’s summarize what we know about these three kinds of acceleration in a chart.

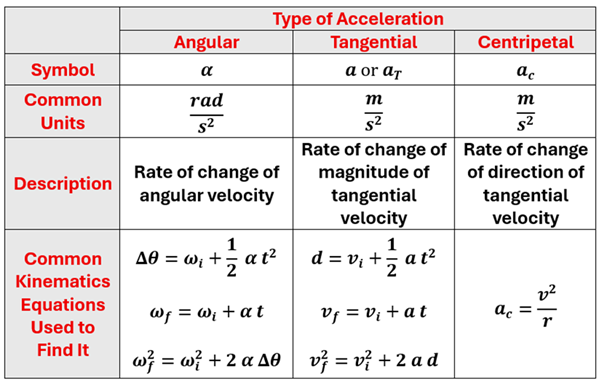
a table of (Rows) Symbols, common units, description and equations for types of acceleration (Columns). For Angular Acceleration, it's symbol if alpha, common units are rad per second squared, description is the Rate of change of angular velocity, and common kinematic equations are 1st delta theta = omega sub i plus one half alpha times t squared. 2nd omega sub f = omega sub i plus alpha times t. 3rd Omega sub f squared = omega sub i squared plus 2 alpha times delta theta. Tangential acceleration has symbols of a or a sub t, common units of meters per second squared, description of the Rate of change of magnitude of tangential velocity, and common equations are 1st d = v sub i plus one half a times t squared. 2nd v sub f = v sub i plus a times t. 3rd v sub f squared = v sub i squared plus 2 a d. Centripetal acceleration has a symbol of a sub c, common units of meters per second squared, description of the Rate of change of direction of tangential velocity, and a kinematic equation of a sub c = v squared over r.

Let’s try an example where we calculate all three.

Example 1: Three Kinds of Acceleration

Problem:  A driver steps on the gas while rounding a curve with a constant radius of 38 m.  The data table provides the car’s speed while taking this curve.  At t = 3.0 s, what are the driver’s
(A) tangential acceleration
(B) angular acceleration
(C) centripetal acceleration?

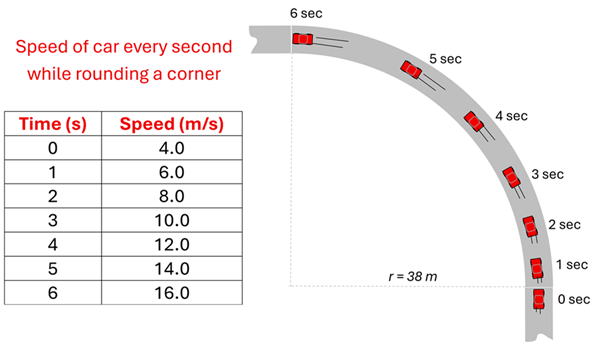
A data table of Time and speed (in meters per second), and a picture of a car going around a 38 meter curve (with 0 seconds being at 0 degrees and 6 seconds being at 90 degrees). The time speed table has (time then speed): 0 4.0, 1 6.0, 2 8.0, 3 10.0, 4 12.0, 5 14.0, and 6 16.0

Solution:  (a) The tangential acceleration can be found by noticing that each second the magnitude of the car’s velocity increases by 2.0 m/s.  Thus, the aT  = 2.0 m/s2. 

The solution for example 1 a. We start with the kinematic equation for translation motion v sub f (velocity final) = v sub i (velocity initial) plus a (acceleration) times t (time). We plug in our Velocity final (16), Velocity initial (4), and time (6) and solve for a which is the same as a sub t, and get 2 meters per second squared.

(b) To find the angular acceleration, we’ll use the tangential acceleration and one of our link equations.  We find ⍺  = 0.053 rad/s2.

Conversion of tangential acceleration to angular acceleration using the equation a (acceleration or tangential acceleration) = r (radius) times alpha (angular acceleration). We put 2 meters per second for a and 38 for the radius and solve to get 0.053 rad per second squared as alpha (angular acceleration)

(c) To find the centripetal acceleration, we use the magnitude of the velocity at t = 3.0 seconds and the radius of curvature to find the centripetal acceleration to be ac  = 2.6 m/s2. 

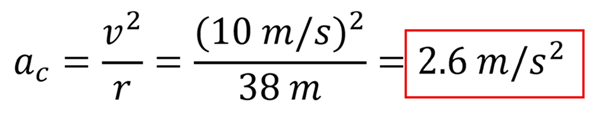
Centripetal acceleration using a sub c (centripetal acceleration) = v (velocity) squared over r (radius) equation, plugging in 10 for the velocity and 38 meters for the radius to get 2.6 meters per second squared.

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.

1. Identify which type of acceleration is experienced by a driver in each of these scenarios.  Write “Yes” or “No” for each of the 3 types of acceleration (Angular, Tangetial/Linear and Centripetal).
(A) A driver in a car takes a curve in the road traveling at a constant speed
(B) A drive in a car speeds up along a straight road
(C) A drive in a car turns round a corner while breaking.

Check Part A Answer

Check Part B Answer

Check Part C Answer

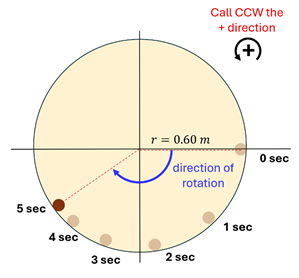
2. A potter’s wheel (radius = 0.60 m) has a ball of clay stuck at the very edge of the clockwise rotating disk.  When turned off, the rotating wheel slows uniformly from 0.95 rad/s to rest in 5.0 seconds.  Determine the magnitude and direction of the:
(A) Angular Acceleration
(B) Tangetial Acceleration at 2.0 seconds
(C) Centripetal Acceleration at 2.0 seconds

the picture of the potters wheel slowing down over 5 seconds. The clay on it starts at 0 and rotates counter clockwise over the 5 seconds.

Check Part A Answer

Check Part B Answer

Check Part C Answer

Next Section:

Tired of Ads?
Go ad-free for 1 year