Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Discovering the Links
A chain is made up of a series of links. What do these links do? In general, they connect things. In this part of our lesson, we are going to discover three very helpful links. What will our links do? They will help us connect rotational quantities that describe an object’s motion to their corresponding translational quantities.
In the previous section we saw that when a point on the rim of a spinning wheel rotates, we described its angular velocity with the variable ω. We learned that we often measure ω in units of radians/sec. But doesn’t this point also have a translational (linear) velocity v that we might measure in m/sec? Indeed, it does. It turns out that these two velocities—the angular velocity ω and the translational velocity v—are related. We can find one if we know the other.
Similarly, during an interval of time, the point on the rim of the wheel rotated through an angle ∆θ. We called this the angular displacement and measured it in units of radians. But doesn’t this black dot on the rim of the wheel below also travel some distance on a curved path along the circumference of the circle that we could measure in meters? It does. We’ll call this distance ∆s. Once again, the angular displacement ∆θ and the distance along the curved arc ∆s are related.
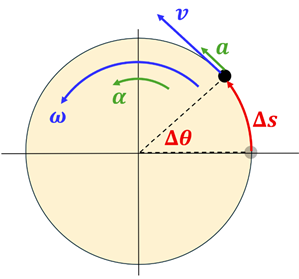
We might also say that, if the spinning dot experiences an angular acceleration (that we could measure in radians/s2), then it will also have a translational acceleration (measured in m/s2). In every case, the rotational quantity of a given point that is rotating is related to its corresponding translational quantity.
We sometimes call the translational velocity of the rotating object its tangential velocity. This makes sense because this velocity is always tangent to the circular orbit. Similarly, we sometimes call the translational acceleration of the rotating object its tangential acceleration. You can see from the picture that it also points tangent to the circle.
The 'Link' Equations
How do we connect these rotational and translational quantities? We do so with the radius—how far the rotating point is from the axis. We can now write three ‘link equations’ that will take us from the rotational quantity to its corresponding translational quantity.
In our previous section we noted that physicists often prefer radians to degrees because using radians offers a more convenient way to move between the rotational and translational quantities. We can now see why by considering the distance link equation above. Let’s say the blue dot, which is 1 m from the axis of rotation, has rotated through an angle of ∆θ =1 radian. Then the distance it traveled (∆s) is 1 m—the same as the radius. This makes sense since this was our definition of a radian from the previous section. Now let’s look at the red dot that also rotated through an angle ∆θ =1 radian. Let’s say the red dot is 2 m from the axis of rotation. We could say that r = 2 m, but more precisely we mean r = 2 m/radius or 2 m/rad. Because of how we define a radian, the ‘radius’ can be replaced with ‘radians.’ Thus, the distance traveled (∆s) by the red dot is 2 m—again, the same as the radius. The radius essentially ‘scales up’ the angular quantity to allow us to determine the translational quantity. The bigger the radius, the bigger the distance traveled along the arc. And since we had measured the angle of rotation in radians, we see how the units conveniently cancel out.
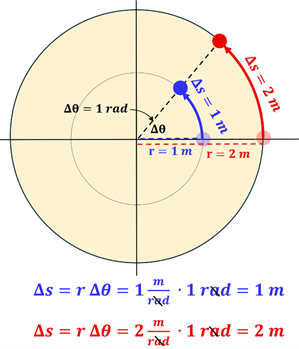
Let’s look at three examples—one for each of the link equations—to see how this works.
Example 1: Finding Arc Length
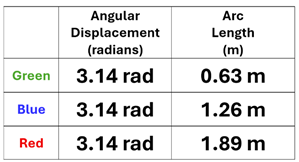
Problem: Three colored dots (green, blue, and red) are fixed to a disk that is allowed to rotate as shown. Each colored dot is a different distance from the axis of rotation. Complete the table below by determining the angular displacement and arc length (or distance) for each.
Solution: All three dots had the same angular displacement as they all rotated 3.14 radians. Using ∆s = r ∆θ, we find that the greater the radius, the greater the arc length traveled.
Example 2: Finding Tangential Velocity
Problem: A child sits 1.5 m from the center of a merry-go-round that is spinning with an angular velocity of 60o/sec. How fast is the child traveling (in m/s) relative to the ground?
Solution: First, let’s convert 60o/s to rad/s. Doing so leads to an angular velocity of 1.05 rad/s. Next, we can think of the radius as 1.5 m/radius or 1.5 m/rad. Since we converted the angular velocity to rad/s, this will allow the ‘rad’ units to cancel. Finally, we’ll use our velocity link equation to determine the magnitude of the tangential velocity to be 1.58 m/s.
Example 3: Finding Tangential Acceleration
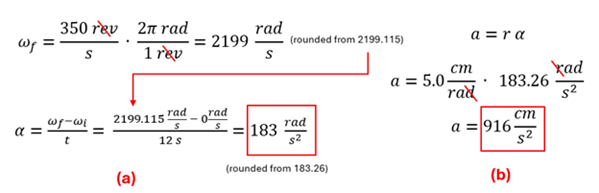
Problem: A centrifuge is used in laboratories to separate substances (often liquids) based on density by rotating rapidly. When turned on, a centrifuge can go from zero to 350 revolutions/sec in 12 seconds. (a) Find the average angular acceleration of the centrifuge during the start-up process, and (b) find the tangential acceleration of the liquid that is 5.0 cm from the axis of rotation during this start-up process?
Solution: (a) First, we’ll find the final angular velocity in rad/s. Next, we’ll use our average angular acceleration equation to find that the angular acceleration during start-up is 183 rad/s2. (b) We can use our acceleration link equation to determine the tangential acceleration of the liquid that is 5.0 cm away from the axis to be 916 cm/s2 .
We Would Like to Suggest ...
Sometimes it isn't enough to just read about it. You have to interact with it! And that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our Rotational Motion Interactive. You can find it in the Physics Interactives section of our website. The Rotational Motion Interactive allows a learner to explore the relationship between a rotating bug’s angular velocity and its tangential (linear) velocity.
Check Your Understanding
Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
1. A red dot on the edge of a wheel or radius 'r' makes one complete revolution. What distance did the red dot travel?
2. At track practice, your teammate says, “I want to run in lane 4 because I get a head start and have to run less distance than those in the inner lanes.” What is the flaw in your teammate’s reasoning?
3. The tub of your washing machine has a diameter of 0.70 m. During the spin cycle, an article of clothing is pinned against the wall of the tub as it makes 5 revolutions/sec.
(A) What is the angular velocity (in rad/s) of the tub during the spin cycle?
(B) How fast (in m/s) is the article of clothing moving during this cycle?
4. Two people (A and B) are standing on a spinning merry-go-round. Person A says, “I have a bigger velocity since I am further from the center.” Person B says, “No, we have the same velocity since we both revolve around the center in the same amount of time.” Who is correct?
5. The figure below shows a top view of a ball attached to a string traveling in a circle. The ball orbits with an angular velocity of ω = 4.0 rad/s. The string is 1.2 m long. The cardinal directions (N, S, E, and W) are shown for reference.
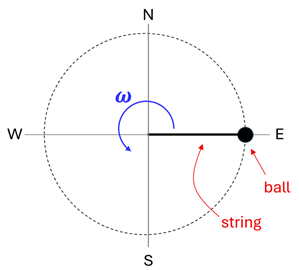
(A) If the string were to break at the moment the ball is in the position shown, what would be the direction of its subsequent motion?
(B) What would be the ball’s velocity (in m/s) immediately after the string breaks?
6. The radius of the Earth is 6.4 x 106 m. If you were standing on the equator of the Earth:
(A) how long would it take for you to make one complete rotation?
(B) what is the magnitude of your angular velocity?
(C) what is the magnitude of your tangential velocity?
7. A large warehouse fan has blades that extend out from the center 1.5 m. What angular acceleration would be necessary so that a point on the rim of the blades has a tangential acceleration equal to the acceleration of gravity on Earth (9.8 m/s2)?
Looking for additional practice? Check out the Calc Pad for additional practice problems.
Figure 1 from MS Word
Figure 2 Picture borrowed from: https://commons.wikimedia.org/wiki/File:202407_Desktop_Centrifuge_Female.svg
Figure 3 author created with person icons from MS Word