Energy Transformation on a Roller Coaster
A roller coaster ride is a thrilling experience which involves a wealth of physics. Part of the physics of a roller coaster is the physics of work and energy. The ride often begins as a chain and motor (or other mechanical device) exerts a force on the train of cars to lift the train to the top of a very tall hill. Once the cars are lifted to the top of the hill, gravity takes over and the remainder of the ride is an experience in energy transformation.
At the top of the hill, the cars possess a large quantity of potential energy. Potential energy - the energy of vertical position - is dependent upon the mass of the object and the height of the object. The car's large quantity of potential energy is due to the fact that they are elevated to a large height above the ground. As the cars descend the first drop they lose much of this potential energy in accord with their loss of height. The cars subsequently gain kinetic energy. Kinetic energy - the energy of motion - is dependent upon the mass of the object and the speed of the object. The train of coaster cars speeds up as they lose height. Thus, their original potential energy (due to their large height) is transformed into kinetic energy (revealed by their high speeds). As the ride continues, the train of cars are continuously losing and gaining height. Each gain in height corresponds to the loss of speed as kinetic energy (due to speed) is transformed into potential energy (due to height). Each loss in height corresponds to a gain of speed as potential energy (due to height) is transformed into kinetic energy (due to speed). This transformation of mechanical energy from the form of potential to the form of kinetic and vice versa is illustrated in the animation below.
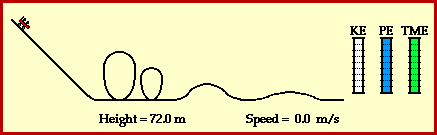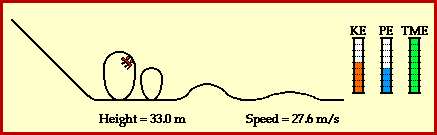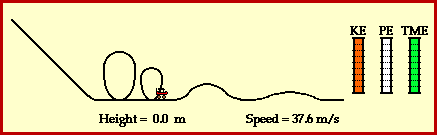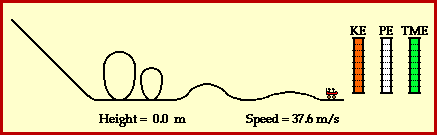
A roller coaster ride also illustrates the work and energy relationship. The work done by external forces is capable of changing the total amount of mechanical energy from an initial value to some final value. The amount of work done by the external forces upon the object is equal to the amount of change in the total mechanical energy of the object. The relationship is often stated in the form of the following mathematical equation.
KEinitial + PEinitial + Wexternal = KEfinal + PEfinal
The left side of the equation includes the total mechanical energy (KEinitial + PEinitial) for the initial state of the object plus the work done on the object by external forces (Wexternal) while the right side of the equation includes the total mechanical energy (KEfinal + PEfinal) for the final state of the object.
Once a roller coaster has reached its initial summit and begins its descent through loops, turns and smaller hills, the only forces acting upon the coaster cars are the force of gravity, the normal force and dissipative forces such as air resistance. The force of gravity is an internal force and thus any work done by it does not change the total mechanical energy of the train of cars. The normal force of the track pushing up on the cars is an external force. However, it is at all times directed perpendicular to the motion of the cars and thus is incapable of doing any work upon the train of cars. Finally, the air resistance force is capable of doing work upon the cars and thus draining a small amount of energy from the total mechanical energy which the cars possess. However, due to the complexity of this force and its small contribution to the large quantity of energy possessed by the cars, it is often neglected. By neglecting the influence of air resistance, it can be said that the total mechanical energy of the train of cars is conserved during the ride. That is to say, the total amount of mechanical energy (kinetic plus potential) possessed by the cars is the same throughout the ride. Energy is neither gained nor lost, only transformed from kinetic energy to potential energy and vice versa.
The conservation of mechanical energy by the coaster car in the above animation can be studied using a calculator. At each point in the ride, the kinetic and potential energies can be calculated using the following equations.
| KE = 0.5 * mass * (speed)^2 |
PE = mass * g * height |
If the acceleration of gravity value of 9.8 m/s/s is used along with an estimated mass of the coaster car (say 500 kg), the kinetic energy and potential energy and total mechanical energy can be determined. What value do you find for the total mechanical energy of the car at any point along the track?
A final feature of the above animation is the use of work-energy bar charts. Work-energy bar charts are a conceptual tool which depict the amount of each form of energy possessed by an object as it an undergoes a particular motion. The work-energy bar charts for the coaster car illustrate that the car's energy is transformed from potential to kinetic and vice versa; yet the total amount of mechanical energy remains the same during the course of the motion.
For more information on physical descriptions of motion, visit The Physics Classroom Tutorial. Detailed information is available there on the following topics:
Potential Energy
Kinetic Energy
Mechanical Energy
Internal vs. External Forces
Work
Work-Energy Theorem
Work-Energy Bar Charts