Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Lesson 2: Acids and Bases in Aqueous Solutions
Part b: The pH Scale in Chemistry
Part a:
Water and its Ionization
Part b: The pH Scale
Part c:
pH Indicators
The Big Idea
Explore how and why the pH scale provides a quantitative measure of acidity or basicity—where neutral water has pH 7, and pH values below or above indicate acidic or basic solutions respectively.
Hydronium and Hydroxide Ion Concentrations
The self-ionization of water to form hydronium ions (H3O+) and hydroxide ions (OH-) was discussed in Lesson 2a. The self-ionization is a reversible system with a very small K value. The ion product constant (Kw) at 25°C is 1.0x10-14 mol2/L2.
[H3O+] x [OH-] = 1.0x10-14 mol2/L2
This means that the concentrations of H3O+ and OH- are typically very low. For neutral solutions, the molar concentrations of these two ions are 1.0x10-7 mol/L. Expressing this value in standard decimal notation helps many students gain a better feel for how miniscule this value is:
[H3O+] = [OH-] = 0.00000010 M
(NOTE: “M” represents mol/L. For more info, see our Solutions Chapter.)
While neutral solutions have equal amounts of hydronium and hydroxide ions, acidic and basic solutions can have unequal amounts of these ions. Here are two of several possible sets of concentration values for acidic and basic solutions that satisfy the ion product constant rule:
Acidic: [H3O+] = 1.0x100 M (a.k.a., 1.0 M), [OH-] = 1.0x10-14 M
Basic: [H3O+] = 1.0x10-14 M, [OH-] = 1.0x100 M (a.k.a., 1.0 M)
pH as a Logarithmic Scale
An inspection of these concentration values leads to at least one obvious conclusion:
There is an enormous range of possible concentrations of hydronium ions and of hydroxide ions in an aqueous solution.
For the concentrations given here, the largest concentration is 14 powers of 10 greater than the smallest concentration. In science, math, and engineering,
a logarithmic scale is often used when dealing with a wide expanse of numerical values. The Richter scale in geology is a logarithmic scale for expressing the amplitude of seismic waves.
The Decibel scale in acoustics is a logarithmic scale for expressing the intensity of sound waves. In Chemistry, the pH scale is a logarithmic scale for expressing the hydronium ion concentration.

So, what is a logarithmic scale? A logarithmic scale, like the
pH scale, is based on powers of 10. In fact, “pH” stands for
powers of hydronium (or powers of hydrogen). The graphic below illustrates the pH scale. For each pH value on the scale, the corresponding molar concentration of H
3O
+ is recorded.

An inspection of the scale shows that a change in the pH by 1 unit corresponds to a change in the H
3O
+ molarity by one power of 10. A change in pH by 2 units corresponds to a change in the H
3O
+ molarity by two powers of 10. A change in pH by 3 units corresponds to a change in the H
3O
+ molarity by three powers of 10. This is why we say that the pH scale is based on powers of 10.
A solution with a pH of 1 is 10
1 times more concentrated with H
3O
+ than a solution with a pH of 2. A solution with a pH of 1 is 10
3 times more concentrated with H
3O
+ than a solution with a pH of 4. And a solution with a pH of 1 is 10
6 times more concentrated with H
3O
+ than a solution with a pH of 7. For any two solutions, the difference in pH is equal to how many powers of 10 times different the H
3O
+ concentration is. The pH scale is based on powers of 10. That’s what
logarithmic means.
In the middle of the scale is a pH of 7. At this pH, the concentration of both H
3O
+ and OH
- is 1.0x10
-7 M. With equal concentrations of the two
opposing ions, the solution is neutral. For pH values below 7, the [H
3O
+] is greater than [OH
-] and the solution is acidic. For pH values above 7, the [H
3O
+] is less than [OH
-] and the solution is acidic. The following table summarizes these relationships.
| pH |
Acidic or Basic? |
[H3O+] to [OH-] Comparison |
| Equal to 7 |
Neutral |
[H3O+] = [OH-] |
| Less than 7 |
Acidic |
[H3O+] > [OH-] |
| Greater than 7 |
Basic |
[H3O+] < [OH-] |
Use the questions in the
Check Your Understanding section to ensure your understanding of these importance concepts about the pH scale.
Calculating the pH from Hydronium Ion Concentration
The equation for pH is
pH = -log [H3O+]
There are two mathematical operations involved in determining the pH from the hydronium ion concentration ([H
3O
+]):
- Take the logarithm of the H3O+ concentration.
- Multiply by -1.
The logarithm function (
log for short)
captures the power on 10 for the molar concentration of H
3O
+. For an aqueous solution with a [H
3O
+] of 1.0x10
-3 M, the pH is 3.00. The determination of the pH of 3.00 is a two-step process as shown below.
Let’s repeat the two-step process to determine the pH if the [H
3O
+] is 1.0x10
-8 M.
Observe how the log function captures the power on 10 of the concentration. It’s conveniently done as head math when the concentration begins with 1.0 x ... .It’s no longer head math when you must determine the pH of an aqueous solution with a [H
3O
+] of 2.5 x10
-3 M. Fortunately calculators are equipped with a log button that can do the work for you. The log of 2.5 x10
-3 is -2.60, so the pH of a solution with a [H
3O
+] of 2.5 x10
-3 M is 2.60.
How to Use Your Calculator to Determine the pH Value
Much of the work of determining pH values from [H
3O
+] will be done using a calculator. The following sequence of buttons would be pressed on a single line scientific calculator to determine the pH if [H
3O
+] = 2.5 x10
-3 M.
The actual appearance and labels of the buttons may vary with calculator brand.
Example 1 – Calculating the pH from [H3O+]
The hydronium ion concentration in a vinegar solution is 4.0x10
-3 M. Determine its pH.
Solution:
This problem can be solved in three simple steps.
- Enter the [H3O+] into your scientific calculator.
- Press the log button to determine the log of this concentration.
- Multiply by -1.
The result is a
pH value of 2.40.
It is worth mentioning that today’s graphing calculators and multi-line scientific calculators allow the three steps to be performed exactly how the equation appears:
Calculating the pOH from Hydroxide Ion Concentration
In addition to the pH scale, there is also a pOH scale. The pOH scale works the same way except that it is based upon the molar concentration of hydroxide ions. The equation for calculating the pOH is
pOH = -log [OH-]
If the [OH
-] is known, then the pOH can be calculated using the same two mathematical operations; take the logarithm of the OH
- concentration and then multiply by -1. For instance, the pOH of an aqueous solution with [OH
-] = 4.9x10
-10 is 9.31.
Example 2 – Calculating the pOH from [OH-]
The hydroxide ion concentration in a Clorox solution is 1.9x10
-4 M. Determine its pOH.
Solution:
This problem can be solved in three simple steps.
- Enter the [OH-] into your scientific calculator.
- Press the log button to determine the log of this concentration.
- Multiply by -1.
The result is a
pOH value of 3.72.
How are pH and pOH Related?
The pH and pOH scales are related by the simple equation:
pH + pOH = 14
If the pH is known, then the pOH can be calculated and vice versa. The table below illustrates the relationship.
| pH |
pOH |
pH + pOH |
Acidic or Basic? |
| 5.0 |
9.0 |
5.0 + 9.0 = 14.0 |
Acidic |
| 11.5 |
2.5 |
11.5 + 2.5 = 14.0 |
Basic |
| 7.0 |
7.0 |
7.0 + 7.0 = 14.0 |
Neutral |
| -1.1 |
15.1 |
-1.1 + 15.1 = 14.0 |
VERY Acidic |
Calculating Concentrations from pH and pOH
Thus far the discussion has been focused on calculating a pH or a pOH value from the concentrations. How would you do the reverse? That is, how would you calculate the concentration of hydronium or hydroxide from the pH or pOH? The equations for doing the reverse (or better named, the inverse) process are:
[H3O+] = 10-pH [OH-] = 10-pOH
Here’s some quick examples of the use of the equation:
- If the pH value is 5.00, then the [H3O+] is 1.0x10-5 M.
- If the pH value is 11.00, then the [H3O+] is 1.0x10-11 M.
- If the pOH value is 4.00, then the [OH-] is 1.0x10-4 M.
- If the pOH value is 1.00, then the [OH-] is 1.0x10-1 M.
- If the pH value is 4.52, then the [H3O+] is 3.0x10-5 M.
- If the pOH value is 9.85, then the [OH-] is 1.4x10-10 M.
The first four bullet points were likely do-able as head math. The last two bullet points require a calculator. The process is shown below. Observe how the last step involves raising 10 to a power equivalent to -1•pH or -1•pOH.
For a scientific calculator, the sequence of button presses for the last example is as follows:
(The appearance of the buttons may vary with calculator brand.)
Putting it All Together
We have developed relationships for molar concentrations and logarithmic values for both hydronium and hydroxide. And previously, we related the concentrations of the two ions to one another. Here is an all-in-one-place listing of our six relationships. All equations are applicable at 25°C. We will assume such temperatures in all problems.
The graphic organizer below lists the four relevant quantities and shows how to determine one quantity from another quantity. Any two quantities connected by a single arrow can be calculated from one another using the equation listed next to the arrow. Any two quantities that are connected by two arrows can be calculated from one another by using two equations.
Example 3 - Relating the pH, pOH, [H3O+], and [OH-]
Express your understanding of pH, pOH, [H
3O
+], and [OH
-] relationships by completing the following table. Tap the
Show Answers button when you are ready to check your answers.
pH of Common Substances
Lesson 1a of this Chapter identified several examples of everyday substances that contain acids and bases. Now that we understand pH, it may be enlightening to place these items on the pH scale. This is shown in the graphic below.
pH and Significant Digits
We have been following the rules -
the significant digit rules. But we haven’t said a word about it. Brace yourself ... here it comes.
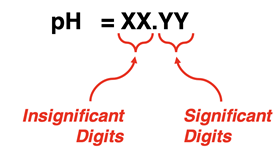
pH is the result of a logarithmic operation. The digits that come before the decimal point in a pH value pertain to the exponent on 10 when expressing the pH in exponential notation. These digits are not significant. The digits that come after the decimal point are the significant digits. So, pH values of 4.25 and 10.75 are each expressed with two significant digits. A pH of 12.1 has one significant digit.
The table below shows some of our results of calculations on this page. The act of using a measured value to perform a calculation should never increase or decrease the amount of precision with which we know a value. For this reason, it is important that the number of significant digits are not changed by doing the calculation. If we know a concentration to two significant digits, then we can know a pH value to two significant digits. Inspect the results and convince yourself that we have followed the rules.
Can the pH be Less than 0 or Greater than 14?
As they appear online and in textbooks, pH scales are often shown as extending from a pH of 0 to a pH of 14. This places a pH of 7 (for neutral) in the exact center of the scale. But it also leaves the incorrect impression that an aqueous solution cannot have a pH that is less than 0 or greater than 14. There is no restriction on high or how low a pH value can be. Many stock solutions of acids and bases in a chemistry store room have pH values that are less than 0 or greater than 14. For instance, chemical suppliers typically ship concentrated HCl solutions having a concentration very close to 12 M. The pH of such a solution is approximately -1.1.
Before You Leave - Practice and Reinforcement
Now that you've done the reading, take some time to strengthen your understanding and to put the ideas into practice. Here's some suggestions.
- Try our Concept Builder titled pH and pOH. Any one of the three activities provides a great follow-up to this lesson.
- Our Calculator Pad section is the go-to location to practice solving problems. You’ll find plenty of practice problems on our Acids and Bases page. Check out the following problem sets: pH and pOH 1 || pH and pOH 2 || pH and pOH 3
- Download our Study Card on pH and pOH. Save it to a safe location and use it as a review tool.
- The Check Your Understanding section below includes questions with answers and explanations. It provides a great chance to self-assess your understanding.
Check Your Understanding of pH Scale and pH-Related Trends
Use the following questions to assess your understanding of key concepts related to the pH scale. Tap the
Check Answer buttons when ready.
1. Read carefully and determine the pH or pOH of Solutions A - F:
- An aqueous solution has a pH of 7.0. What is the pH of Solution A if its [H3O+] is 10 times greater?
- An aqueous solution has a pH of 7.0. What is the pH of Solution B if its [H3O+] is 1000 times greater?
- An aqueous solution has a pH of 7.0. What is the pH of Solution C if its [H3O+] is 100 times less?
- An aqueous solution has a pH of 7.0. What is the pH of Solution D if its [H3O+] is 10000 times less?
- An aqueous solution has a pH of 7.0. What is the pOH of Solution E if its [H3O+] is 1000 times greater?
- An aqueous solution has a pH of 7.0. What is the pOH of Solution F if its [H3O+] is 100 times less?
2. Complete the following statements regarding Solutions A - D.
- Aqueous solution X has a pH of 5.0. Solution A has a pH of 3.0. Solution A is _______ (more, less) concentrated with H3O+ by a factor of _______ (0.2, 2, 20, 100, 1000).
- Aqueous solution X has a pH of 5.0. Solution B has a pH of 7.0. Solution B is _______ (more, less) concentrated with H3O+ by a factor of _______ (0.2, 2, 20, 100, 1000).
- Aqueous solution X has a pH of 5.0. Solution C has a pH of 1.0. Solution C is _______ (more, less) concentrated with H3O+ by a factor of _______ (0.4, 4, 40, 100, 10000).
- Aqueous solution X has a pH of 5.0. Solution D has a pH of 9.0. Solution D is _______ (more, less) concentrated with H3O+ by a factor of _______ (0.4, 4, 40, 100, 10000).
- Aqueous solution X has a pH of 5.0. Solution E has a pH of 3.0. Solution E is _______ (more, less) concentrated with OH- by a factor of _______ (0.2, 2, 20, 100, 1000).
- Aqueous solution X has a pH of 5.0. Solution F has a pH of 7.0. Solution F is _______ (more, less) concentrated with OH- by a factor of _______ (0.2, 2, 20, 100, 1000).
3. Fill in the blank paragraph about pH scale:
The pH scale is a ________ (linear, logarithmic) scale. Two pH values that differ by 2.0 units represent solutions that have a ________ (2:1, 20:1, 100:1) ratio of hydronium ion concentrations. A solution with a pH of 7.0 is considered _________ (acidic, basic, neutral). A solution with a pH of 3.0 is considered _________ (acidic, basic, neutral). And a solution with a pH of 12.0 is considered _________ (acidic, basic, neutral). As the [H
3O
+] increases, the [OH
-] __________ (increases, decreases, remains constant) and the pH value __________ (increases, decreases, remains constant). For any solution at 25°C, the pH and the pOH values _____________ (are equal, are reciprocals, add to 14.0).
4. For Solutions A, B, and C, decide which one is most acidic.
- Solution A: pH = 3.10
- Solution B: [H3O+] = 1.5x10-13 M
- Solution C: [H3O+] = 8.5x10-2 M
5. For Solutions A, B, and C, decide which one is most acidic.
- Solution A: pH = 13.50
- Solution B: [H3O+] = 1.5x10-10 M
- Solution C: [OH-] = 8.5x10-8 M
6. For Solutions A, B, and C, decide which one is most acidic.
- Solution A: pOH = 11.90
- Solution B: [H3O+] = 2.2x10-5 M
- Solution C: [OH-] = 1.6x10-9 M
7. Express your understanding of pH, pOH, [H
3O
+], and [OH
-] relationships by completing the following table.
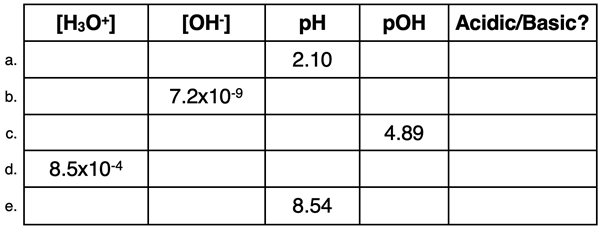
8. Louie Kaliente loves a spicey hot pepper. His favorite is packed with acid, giving it a pH value of 4.70. Calculate the hydronium ion concentration in the pepper.
9. In another episode of Chemistry for Better Living, Julia and her Dad purchased a bottle of Muriatic Acid at the local hardware store in order to clean the concrete surface on their backyard basketball court. The label indicated that it had a pH of 2.25. Assuming a temperature of 25°C, calculate …
a. … the pOH of the solution.
b. … the hydronium ion concentration of the solution.
c. … the hydroxide ion concentration of the solution.