Lesson 2: Acids and Bases in Aqueous Solutions

Part a: Water and its Ionization

Part a: Water and its Ionization
Part b: The pH Scale
Part c: pH Indicators

 

The Big Idea

Discover how water self-ionizes into hydronium (H₃O⁺) and hydroxide (OH^-), establishing the crucial ion-product constant (Kw = 1 × 10^-14 at 25 °C) that underlies acid-base equilibrium in aqueous solutions.

 

Self-Ionization of Water

Chapter 15 focuses on aqueous solutions of acids and bases. At the heart of this topic is water and its tendency to undergo self-ionization. Molecules of water are in constant random motion about the solution. The collision of two water molecules with the proper orientation and sufficient energy will result in a reaction in which a proton (H⁺ ion) is transferred from one molecule to the other molecule.

H₂O(l)  +  H₂O(l)     ⇄    H₃O⁺(aq)  +  OH^-(aq) 

 
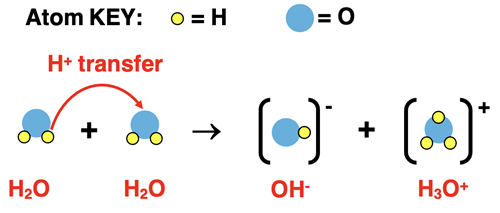
The reaction, referred to as a self-ionization reaction, demonstrates water’s amphiprotic qualities. Water is acting as both a proton donor and a proton acceptor. Upon donating a proton to another water molecule, H₂O turns into its conjugate base (OH^-), the hydroxide ion. And upon accepting a proton, a water molecule turns into its conjugate acid (H₃O⁺), the hydronium ion. Because this self-ionization of water inevitably occurs in every aqueous solution, these two ions are always present. As we will soon see, their prevalence in solution is a signature of the acidity and pH level of that solution.
 
 
 

An Equilibrium System

The self-ionization of water is a reversible reaction. That is, not only do two water molecules collide to produce the ions, the ions will collide quite regularly to reform the water molecules. In fact, the reverse reaction is a dominant reaction and the equilibrium lies far to the left. The self-ionization equilbrium is best represented as follows:

 
As we learned in the Equilibrium Chapter of our Chemistry Tutorial, the value of the equilibrium constant (K) provides a measure of whether the equilibrium favors the formation of products or reactants. A relatively low K value (K <<< 1) indicates a weak forward reaction; the equilibrium favors reactants. For the self-ionization of water, the K value is 1.0x10^-14 at 25°C. Because the K value is so low, the concentrations of the two ions are typically small.
 
The equilibrium constant equation can be written as

K_w = [H₃O⁺]•[ OH^-] = 1.0x10^-14 mol²/L² 

 
The symbol K_w is used specifically for water’s self-ionization reaction. It is sometimes referred to as the ion product constant, referring to the product of the ion concentrations.
 
Because this equilibrium system is always present in any aqueous solution, the relationship

1.0x10^-14 mol²/L²  =  [H₃O⁺]•[ OH^-]

will always be an accurate description of the solution. If OH^- ions are added to the solution, the equilibrium will undergo a LeChatelier shift to establish a new equilibrium position in which the product of the two ion concentrations is equal to the K_w value. Similarly, if H₃O⁺ ions are added to the solution, there will be a LeChatelier shift to re-establish an equilibrium that satisfies the above mathematical statement. There is no means of escaping the ion product constant. The product of the two ion concentrations is always equal to 1.0x10^-14 mol²/L² (assuming 25°C).

 
 

 
 

Acidic, Basic, and Neutral Solutions

The two ion products of water’s self-ionization are the same ions produced when an acid or a base undergoes dissociation in water. For instance, the hydronium ion is produced by the dissociation of hydrofluoric acid (or any other acid):

HF(aq)  +  H₂O(l)    →    F^-(aq)  +  H₃O⁺(aq) 

And the hydroxide ion is produced by the dissociation of the ammonia (or any other base):

NH₃(aq)  +  H₂O(l)    →    NH₄⁺(aq)  +  OH^-(aq) 

 
So, adding an acid or a base to pure water increases the concentration of one of these two ions and shifts the equilibrium so that the product of ion concentrations is equal to the K_w value of 1.0x10^-14. We can use the ion product concentration to relate the acidity or basicity of solution to the relative concentrations of hydronium and hydroxide ions. Here’s three rules for doing so:

• If [H₃O⁺] = [OH^-], then the solution is neutral.
• If [H₃O⁺] > [OH^-], then the solution is acidic.
• If [H₃O⁺] < [OH^-], then the solution is basic.

 
We can represent these ideas in a conceptual manner with the following bar charts. The height of the bars provides a measure of the relative amount of hydronium and hydroxide ion concentrations.
   
For highly acidic solutions, the hydronium ion concentrations can be several powers of 10 greater than the hydroxide ion concentrations. A more quantitative representation of the relative concentrations is shown in the table below. Note that in all situations, the product of the two ion concentrations is equal to the K_w value.
   
 
 

Calculating Hydronium and Hydroxide Ion Concentrations

The ion product constant (K_w value) allows one to calculate the concentration of hydroxide ions if the concentration of hydronium ions is known, and vice versa. The product of the two concentrations must equal 1.0x10^-14. (We will assume all concentrations are molar concentrations; that is, mol/L.) The algebraically manipulated equations are shown below:
   
 
 

Example 1: Calculating Hydroxide Ion Concentration

Anna Litical mixes up a solution of 0.025 M hydrochloric acid. Its hydronium ion concentration is 2.5x10^-2 M. Calculate its hydroxide ion concentration.
 

Solution:

Given: [H₃O⁺] = 2.5x10^-2 M
Determine: [OH^-]
 
Using the equation above right, the hydronium ion concentration can be substituted into the denominator. Using a calculator, the hydroxide ion concentration can be calculated. The result is shown below:
   
 
When using scientific notation on your calculator (particularly scientific calculators), caution should always be given to how a number expressed in scientific notation is entered. The sequence of keys to be pressed to enter 1x10^-14 are shown below. Note that the X and 10 (for times 10) keys are never pressed. The EE function key performs that operation instead.    
 
 

Example 2: Calculating Hydronium Ion Concentration

Sal Lushun prepares a solution of a base with a hydroxide ion concentration of 0.012 M. Determine the hydronium concentration of the solution.
 

Solution:

Given: [OH^-] = 0.012 M
Determine: [H₃O⁺]
 
Using the equation for hydronium ion concentration, the hydroxide ion concentration can be substituted into the denominator. Using a calculator, the hydronium ion concentration can be calculated. The result is shown below:
   
 
 
 

Before You Leave - Practice and Reinforcement

Now that you've done the reading. Take some time to strengthen your understanding and to put the ideas into practice. Here's some suggestions.
 

• The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.
• Download our Study Card on The Ion Product Constant. Save it to a safe location and use it as a review tool. (Coming Soon.)

 
 
 
 

Check Your Understanding the Self-Ionization of Water

Use the following questions to assess your understanding of concepts associated with the ion product constant and the self-ionization of water. Tap the Check Answer buttons when ready.
 
1. Complete the following statements.
a. As the [H₃O⁺] increases, the solution becomes _______ (more, less) acidic.

b. As the [OH^-] increases, the solution becomes _______ (more, less) acidic.


​

c. As the [H₃O⁺] increases, the solution becomes _______ (more, less) basic.


​

d. As the [OH^-] increases, the solution becomes _______ (more, less) basic.


​

e. If [H₃O⁺] is greater than 1.0x10^-7 M, then the solution is ________ (acidic, basic).


​

f. If [OH^-] is greater than 1.0x10^-7 M, then the solution is ________ (acidic, basic).
 

​


 
 
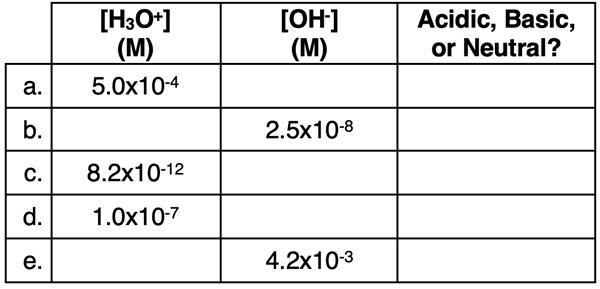
2. Perform calculations to complete the following table.

 
 

​