Lesson 2: Spontaneity and Entropy

Part c: Mathematics of Entropy Change

Part a: Driving Forces for Change
Part b: What is Entropy?
Part c: Mathematics of Entropy Change
Part d: The Second Law of Thermodynamics

 

The Big Idea

Entropy can be measured, not just described. By using standard molar entropies and the Third Law of Thermodynamics, chemists can calculate ΔS for the system, helping to explain the driving forces behind spontaneous change.
 

 

Entropy and Entropy Change

In Lesson 2b, we discussed both a simplified and accessible definition of entropy and a more formal and accurate definition of entropy. Our simplified definition described entropy as a measure of the degree to which the parts of a system are disordered, disorganized, dispersed, or randomly arranged. The more formal definition described entropy as a measure of the number of possible microstates of atoms and molecules within the system that are consistent with the macroscopic observations of the system. (Read more about ...   the simple concept and the formal definition.)
 
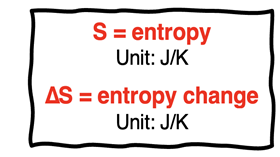Our discussion of entropy in Lesson 2b was not mathematical. Yet, entropy is a quantity that can be measured and quantified. On this page, we will learn how to determine the quantity entropy change for a system undergoing a chemical or a physical change. In our discussion, entropy is represented by the symbol S and has units of J/K (joule per kelvin). Entropy change will be represented by the symbol ∆S.
 
 

 

The Third Law of Thermodynamics

A discussion of the quantitative nature of entropy begins with the third law of thermodynamics.

The third law gives us a starting point for thinking quantitatively about entropy. If a pure solid could be brought to a temperature of 0 K, its entropy would be the lowest possible value of zero. This ability to assign a numerical value to the entropy of a substance makes the quantity entropy much different than the quantity enthalpy introduced in Chapter 12 of this Chemistry Tutorial. The enthalpy scale is based upon an arbitrary zero point. We assign a 0-kJ value to the enthalpy of every element in its standard state. So, Cu(s) and O₂(g) and Hg(l) have an enthalpy of 0 kJ at 25°C and 1 atm because we said so. And the enthalpy of all other substances are determined by relative to these arbitrarily assigned 0 values. But for entropy, we have a value of 0 J/K for a solid crystal at 0 K because there is literally no entropy (no disorder and a single microstate) at that temperature. The entropy scale has a true zero point. The entropy of any other substance in any state at any temperature is expressed relative to this zero point.
 
 
 

Temperature Changes, State Changes, and Entropy Changes

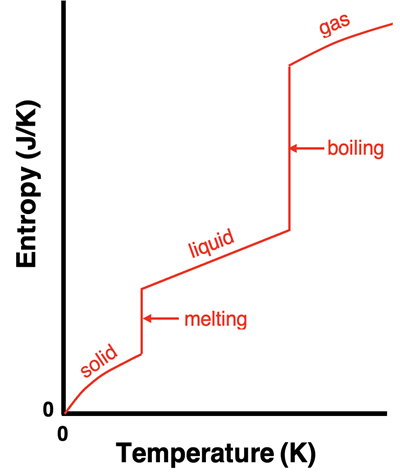In Lesson 2b, we discussed the effect of temperature and the state of matter upon entropy. As heat is added to a substance, its temperature increases and its particles display an increase in the average kinetic energy of motion. This increasing temperature allows the substance to assume a greater number of microstates and causes an increase in entropy. The relationship between entropy and kelvin temperature is approximately linear, especially for liquids; there are very minor deviations from linearity for solids and gases.
 
Changes of state occur at a constant temperature. (Review: Energy and Changes of State.) Different states of the same substance have different entropy values. The entropy of the gaseous state is greater than the entropy of the liquid state which is greater than the entropy of the solid state. During a change of state, the temperature remains steady while the entropy changes.
 
 
 

 
 

Calculating an Entropy Change

Though the method is beyond the scope of this Tutorial, the entropy of a substance can be determined at a standard temperature and pressure (25°C and 1 atm). Entropy values for 30 substances under standard conditions are shown in the table below. They are listed in the table on a per mole basis. See our Reference page for entropy values for nearly 1000 substances. 
 

 
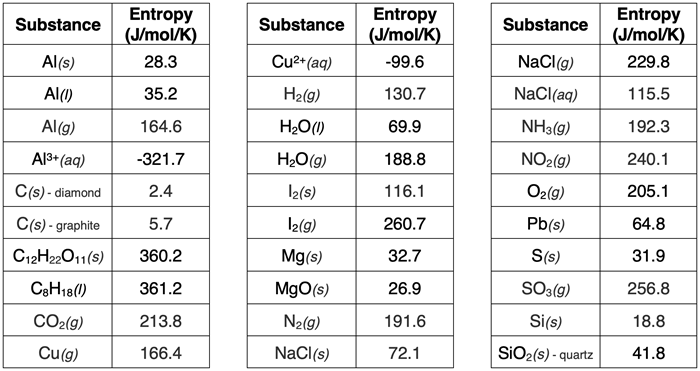
Like enthalpy, entropy is a state function. Entropy values for reactants and products can be used to determine the entropy change of a reaction. The entropy change of any reaction is the sum of the S° values of all the products minus the sum of the S° of all reactants. In equation form

∆S°_reaction  =  ∑ S°_products  -  ∑ S°_reactants

 

When using this equation, be sure to …

• Multiply S° values by the coefficients in the balanced chemical equation. The S° values are expressed on a per mole basis. A multiplier must be used if there is more than one mole listed in the balanced chemical equation.
• Pay attention to the state symbol when looking up entropy values in a table. The entropy varies from solid to liquid to gas.
• Subtract the total or sum (∑) for the reactants from the total or sum (∑) of the products.
• Be very careful about + and - signs. The equation is not a rocket science equation; but it is an equation that requires attention to details.
• The units provided for entropy in reference tables (like the one above or in our Reference section) are J/mol/K. One you have multiplied by moles (first bullet point), you will have determined the entropy change in J/K. If you need to know the value in kJ/K, you will need to divide by 1000.

 
We will demonstrate the use of this equation in the following examples.
   
 

Example 1 - Calculating the ∆S of a Reaction

Ammonia is synthesized according to the reaction
   
Use the values in the above table to determine the entropy change for this reaction under standard conditions.
 
 

Solution

The three entropy values are:
 
The entropy change can be calculated using the equation:
   
Coefficients of 1, 3, and 2 will need to be used as multipliers. Substitution leads to the following equation:
   
The two terms inside the brackets must be added together and then the sum is subtracted from the first term. The solution continues as follows:
   
 
 

Example 2 - Calculating the ∆S of a Reaction

Coal deposits contain sulfur. When burned, sulfur trioxide is often formed from the combustion of the sulfur (along with sulfur dioxide). Upon exiting a smoke stack, SO₃ readily reacts with water vapor to produce sulfuric acid (H₂SO₄), leading to an environmental problem known as acid rain. The reaction that produces SO₃ is:
   
Use the values in the above table to determine the entropy change for this reaction under standard conditions.
 
 
Solution
The three entropy values are:
 
The entropy change can be calculated using the equation:
   
Coefficients of 2, 3, and 2 will need to be used as multipliers. Substitution leads to the following equation:
   
The two terms inside the brackets must be added together and then the sum is subtracted from the first term. The solution continues as follows:
   
 
 

Example 3 - Calculating the ∆S of a Reaction

The combustion of octane gasoline occurs as follows:
   
Use the values in the above table to determine the entropy change for this reaction under standard conditions.
 
 

Solution

The four entropy values are:
The entropy change can be calculated using the equation:
   
Coefficients of 2, 25, 16, and 18 will need to be used as multipliers. Substitution leads to the following equation:
   
The two terms inside the brackets must be added together and then the sum is subtracted from the sum of the first two terms. The solution continues as follows:
   
 
 

Next Up

Lesson 2 is all about spontaneity and entropy. We have discussed matter spread and energy spread as two driving forces of reaction. We have introduced the concept of entropy and have learned how to calculate a system’s entropy change. In Lesson 2d we will tie it all together with a discussion of the second law of thermodynamics. But before you leave, take some time to develop the skill of calculating entropy change.
 
 
 
 
 

Before You Leave - Practice and Reinforcement

Now that you've done the reading, take some time to strengthen your understanding and to put the ideas into practice. Here's some suggestions.
 

• The Check Your Understanding section below includes questions with answers and explanations. It provides a great chance to self-assess your understanding.
• Download our Study Card on Determining Entropy Change. Save it to a safe location and use it as a review tool. (Coming Soon.)

 
 
 

Check Your Understanding of Entropy Change

Use the following questions to assess your understanding of entropy, entropy change, and entropy change calculations. Tap the Check Answer buttons when ready.
 
1. We have learned that the entropy of a gas is greater than the entropy of a liquid which is greater than the entropy of a solid.  Find some data in the table of entropy values that support this idea.

 
 
2. System A contains 1 mole of N₂(g) and 2 moles of O₂(g). System B contains 2 moles of NO₂(g). Each has the same number of each type of atoms. They are simply configured differently in the two systems. Perform a calculation of the entropy of System A and of System B. Identify the system with the greater entropy. Then associate this conclusion with the concepts presented in Lesson 2b on entropy.

​

 
 

3. Consider the sublimation of iodine.
a. Write the chemical equation for this change of state.



b. Use the table of entropy values above to calculate the entropy change. 



c. Does your calculated ∆S value represent an entropy increase or decrease? Explain. 



d. Provide some conceptual reasoning based on the information in Lesson 2b for why the entropy increased or decreased. 

 


 
4. Consider the combustion of solid magnesium to produce magnesium oxide.
a. Write the chemical equation for this reaction.

 


b. Use the table of entropy values above to calculate the entropy change.

 


c. Does your calculated ∆S value represent an entropy increase or decrease? Explain.

 


d. Provide some conceptual reasoning based on the information in Lesson 2b for why the entropy increased or decreased.

 


 
 
5. The electrolysis of liquid water occurs as follows:

2 H₂O(l)  →  2 H₂(g)  +  O₂(g)   

Use the table of entropy values above to calculate the entropy change for this reaction.

​