Lesson 2: Spontaneity and Entropy

Part b: What is Entropy?

Part a: Driving Forces for Change
Part b: What is Entropy?
Part c: Mathematics of Entropy Change
Part d: The Second Law of Thermodynamics

 

The Big Idea

Entropy increases when matter and energy spread out. Melting, vaporizing, warming, and mixing all lead to more dispersal of particles, which means more entropy. This increase reflects the greater number of ways the system can be arranged, making high-entropy states more probable than low-entropy ones.
 

 

Simplified vs. Formal Definitions of Entropy

In Lesson 2a, the concepts of energy spread and matter spread as driving forces of reactions was discussed. These concepts are closely related to a thermodynamic property known as entropy. Entropy is defined in formal terms as

 
While this definition is accurate, it is generally useless to most beginning students of chemistry. Our goal is to move closer towards understanding this formally worded definition. But to do so, we have to begin with a more accessible translation of it. We admit that such translations do run the risk of trading some accuracy for accessibility. But we do need a softer starting point that a student can sink their teeth into. Our initial working definition of entropy is: Entropy is a measure of the degree to which the parts of a system are disordered, disorganized, dispersed, or randomly arranged. For the sake of simplicity, this is a better starting definition. Let’s unpack it and then we’ll apply it to chemical and physical systems.
 
 
 

 

Thinking Conceptually About Entropy

Every so often, my workshop gets organized. The screwdrivers get put away with the other screwdrivers. The wrenches are gathered together and put in their place. The saws are hung back on the hooks in the closet. Mounds of sawdust are swept up and thrown away. Glues and adhesives are collected and put back in their respective storage bins. Table surfaces are cleared of all nails, screws, tape, and other debris. After spending an hour or more of energy organizing the workshop, everything is in its place and ordered. At that point, we would describe the workshop as being in a state of low entropy. All the parts of the workshop are ordered, organized, and thoughtfully arranged.
 
Then the workshop gets used. Projects are done. Screwdrivers, wrenches, saws, glues, adhesives, nails, and screws are pulled from their storage locations. After use, they’re not put back or are seldom put back. The degree of disorder, disorganization, and dispersal of tools and parts increases with time. After a couple of months, the workshop is once again in a state of high entropy.

 
The fate of the workshop is likely similar to experiences in your life. Think about your room, your closet, your desk, your locker, your drawers. Over time, they tend towards high entropy states - disorganized, disordered, dispersed, and randomly arranged. It’s not difficult to see the close connection between the concept of matter spread introduced in Lesson 2a and the entropy concept discussed on this page. Matter spread and entropy increases tend to occur naturally. It takes some energy and outside intervention to decrease a system’s entropy and restore it to an organized state.
 

 

 

The Entropy of Chemical Systems

There are two common entropy goals in most Chemistry courses for which we wish to prepare you:

• to compare the entropy of two different chemical systems,
• to identify the change in entropy as an increase or a decrease for a system undergoing a chemical or a physical change between two different states.

 
To accomplish these goals, you need to consider the degree to which the particles in the system are organized or arranged. Inspect the degree of motion of the particles. Particles with a high degree of motion are able to arrange themselves in a variety of ways and assume high entropy states. Inspect any constraints like bonds or intermolecular forces that restrict motion and the ability of particles to disorder, disorganize, and assume multiple spatial arrangements. Systems which offer constraints and restrictions on particle motion tend to be less disordered and have lower entropy. Consider how dispersed or intermingled that the particles of the system are; dispersal of particles corresponds to higher entropy states. Any property of a system that allows its particles to move about, to mix, to spread, to disperse, to disorganize, and to assume multiple spatial arrangements is a property that is characteristic of higher entropy.
 
 
 

Entropy and the State of Matter

The solid, liquid, and gaseous state of all substance have different levels of entropy. As we learned in Chapter 2 of our Chemistry Tutorial, these three states of matter have unique particle properties. The particles of a solid are held tightly in place by relatively strong intermolecular forces. This gives solids a highly organized structure and allows its particles no ability to move about and assume different spatial arrangements. Solids have low entropy. On the other end of the states-of-matter-spectrum, the particles of an ideal gas experience no intermolecular forces. There are no constraints upon how they move or how they are organized. Gases are characterized by random particle motion - vibration, rotation, and translation. As such, gases have a higher entropy than liquids and solids.
   
 
 

Entropy and Mixing or Dissolving

Consider a system composed of two types of parts - for instance, a container of red balls and blue balls. A high entropy arrangement of the parts would be one in which the individual parts are mixed together. When the red balls and blue balls are dispersed through the entire system, there is a large degree of disorder and the entropy is high. But if the red balls are separated from the blue balls and there is little mixing, the organization is high and the entropy is low.
   
We can related this idea to chemical and physical phenomenon like the dispersal of a gas about the entire container or the dissolving of a solute within a solvent. Mixing and dissolving are examples of matter spread and lead to higher entropy states.
   
 
 
 

Entropy and Atomic Organization

We learned in Chapter 2 of this Chemistry Tutorial that an atom can bond together with other atoms to form molecules. Let’s consider a sample of 10 isolated nitrogen (N) atoms. Nitrogen is an element that naturally forms diatomic molecules, N₂. Our small sample of nitrogen could exists as 10 isolated atoms (10 N) or as five diatomic molecules (5 N₂). Which would have the greater entropy? The bond between nitrogen atoms imposes a constraint upon the nitrogen. The atoms are now a single unit and must move about together. Wherever one atom goes, its bonded pair must go with it; that’s a constraint. This limits the number of ways that those two nitrogen atoms can arrange themselves within the container. Two isolated nitrogen atoms have no constraints upon their motion. One can be on the left side of the container while the other is on the right side of the container. So, 10 N has a greater entropy than 5 N₂.
   
Similar reasoning allows us to compare the entropy of 2 C + 4 H₂ to 2 CH₄. In the case of 2 C + 4 H₂, there are six particles. And in the case of 2 CH₄, there are two particles. From an elemental viewpoint, there are the same number of atoms of the two elements in each sample. But the manner in which the atoms are arranged to form molecules affects the overall entropy of the system. As bonds from between atoms to produce molecules, those bonds impose constraints upon the ability of the atoms to move about the system. This gives the system more organized structure and limits the number of ways that the atoms can arrange themselves in a disordered fashion.
   
When it comes to particle complexity, single atoms (as opposed to complex molecules) are the simplest, least complex of all particles. Their simplicity tends to contribute to a higher entropy. On the other hand, large, multi-atom molecules have more structure (relative to their independent atoms) and prevent their atoms from widespread dispersal about the container. Such complex molecules have a lower entropy.  
 

Entropy and Temperature

Temperature is another factor that contributes to the entropy of a system. As we learned in Chapter 12 of our Chemistry Tutorial, a thermometer reading is like a speedometer reading. It communicates information about the relative amount of kinetic energy of the particles in the system. If the system is a liquid or gas, the increase in temperature would cause its particles to move from one location to another at a greater average speed. And for solids, an increase in temperature would cause the particles to vibrate more vigorously about their fixed positions. In all cases, a greater temperature leads to increased disorder, matter dispersal, or randomness. Entropy increases with increasing temperature.
 
 
 

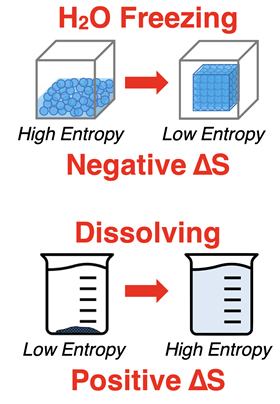Entropy Change

Systems often undergo chemical and physical changes. It is common to observe the components of a system mixing, dissolving, expanding, dispersing, heating, cooling, and reacting. These changes result in changes in entropy. Any change that causes the system’s entropy to increase has a positive entropy change. And any change that causes the system’s entropy to decrease has a negative entropy change.
 
To determine the positive or negative nature of the entropy change, compare the initial and final state of the system. If the final state has a greater entropy than the initial state, then there is a positive entropy change (i.e., entropy increase). If the final state has a smaller entropy than the initial state, then there is a negative entropy change (i.e., an entropy decrease). Two examples are provided at the right.
 
(Note that S is the symbol for entropy and ∆S represents the entropy change. )
 
 


 
   

 

 
 

Next Up

Entropy is actually a quantity. On the next page of Lesson 2, we will learn how to determine the entropy of a system of reactants and products and the entropy change for a chemical reaction. But before you rush forward, make sure you understand this lesson. The Before You Leave section includes several ideas for reinforcing your learning.
 
 
 
 

Before You Leave - Practice and Reinforcement

Now that you've done the reading, take some time to strengthen your understanding and to put the ideas into practice. Here's some suggestions.
 

• Try our Concept Builder titled Entropy. Any one of the three activities provides a great follow-up to this lesson.
• The Check Your Understanding section below includes questions with answers and explanations. It provides a great chance to self-assess your understanding.
• Download our Study Card on Entropy. Save it to a safe location and use it as a review tool. (Coming Soon.)

 
 
 

Check Your Understanding of Entropy

Use the following questions to assess your understanding of the entropy concept. Tap the Check Answer buttons when ready.
 
1. Which of the following statements are true about entropy? Select all that are TRUE.

1. Entropy is a statistical version of enthalpy.
2. An object that is not moving has zero entropy.
3. Highly disordered states have relatively high entropy.
4. A gas changing to a solid is an example of a negative entropy change.

 

 
 
2. For the following pairs of contrasting system configurations, identify which has a higher entropy.
System A: A flask of vaporized I₂.
System B: A flask of I₂ crystals.

  ​

 
System C: 2 H₂O(g)
System D: 2 H₂(g)  +  O₂(g)
 
  ​

 
System E: Air at 20°C.
System F: Air at 90°C

  ​

 
System G: CuSO₄(s) + 1.0 L H₂O(l)
System H: 1.0 L of CuSO₄(aq)
 
  ​

 

3. Describe the following chemical and physical changes as having either a positive or a negative entropy change:

1. Water is boiled. 
   
   Check Answer
   Answer: Positive ∆S
   
   This is a physical change of a liquid into a gas. A gas has a higher entropy than a liquid. So, the change is from a relatively low entropy to a higher entropy state. That's a positive entropy change.
   
    
   
    
2. Sugar is dissolved in iced tea. 
   
   Check Answer
   Answer: Positive ∆S
   
   Dissolving involves dispersing a solid about a solvent. This is a change from a highly-organized, low entropy state to a very disorderd and relatively high entropy state. That's a positive entropy change.
   
    
   
    
3. A gas diffuses to fill a room. 
   
   Check Answer
   Answer: Positive ∆S
   
   The diffusion of a gas is an example of matter spread or dispersal of a substance across a wider area. This is a change from a low entropy state (concentrated and ordered) to a higher entropy state. Thus, there is a positive entropy change.
   
    
   
    
4. Water vapor condenses on the side of a container. 
   
   Check Answer
   Answer: Negative ∆S
   
   Condensation is a change from the gaseous state to the liquid state. Gases are higher entropy than liquids. And so, this physical change represents a loss of entropy or a negative entropy change.
   
    
   
    
5. A wood log is burned in a fireplace to produce CO₂, H₂O, and ashes. 
   
   Check Answer
   Answer: Positive ∆S
   
   CO₂, H₂O, and ashes are considerably more dispersed and disordered than a wood log. Thus, the chemical reaction proceeds from low entropy to high entropy.