Lesson 1: A Model of Solutions

Part d: Solubility, Temperature, and Pressure

Part a: What is a Solution?
Part b: Solubility and Structure
Part c: The Dissolving Process
Part d: Solubility, Temperature, and Pressure
Part e: Dissociation of Ionic Compounds

 

Effect of Temperature on Salt Solubility

Solubility refers to the maximum amount of solute that can be dissolved in a specified amount of solvent. The actual solubility value depends on the solute and the solvent. But it also depends upon temperature. For ionic solids or salts, the solubility in water is most often observed to increase with increasing temperature. But there are other salts whose solubility in water is observed to decrease with increasing temperature.

 
The explanation of temperature effects on salt solubility in water usually relies on LeChatelier’s Principle - a principle to be discussed in Chapter 15 of this Chemistry Tutorial. We will save that explanation for Chapter 15. For now, we will use a particle level explanation.
 
As discussed in Lesson 1c, dissolving a salt in water involves two steps:

1. Ions are pulled away from the crystal lattice (an endothermic step related to lattice energy).
2. Separated ions are attracted to and surrounded by water molecules (an exothermic step related to solvation energy or hydration energy).

 
 For many salts, the lattice energy (step 1) is so great that the overall dissolving process is endothermic. These salts are the ones whose solubility is typically increased by increasing temperatures. At higher temperatures, water molecules move about the container with greater speeds and kinetic energy. These increased speeds allow water to be more effective at penetrating the surface of the crystal and pulling ions away from the lattice and into the solution. And with a greater speed, water molecules can pull the solvated ion away from the crystal more quickly and reduce the likelihood of recrystallization.
 
Some salts are less soluble in water at higher temperatures. This is most commonly observed of salts with such a large solvation energy (step 2) that the overall dissolving process is exothermic. For such salts, the higher speeds of water molecules at higher temperatures makes them less able to keep the solvated ions stabilized. Solvated ions are more likely to escape water’s hold on them and recrystallize. This lowers the solubility at higher temperatures.
 
 
 

Solubility Curves

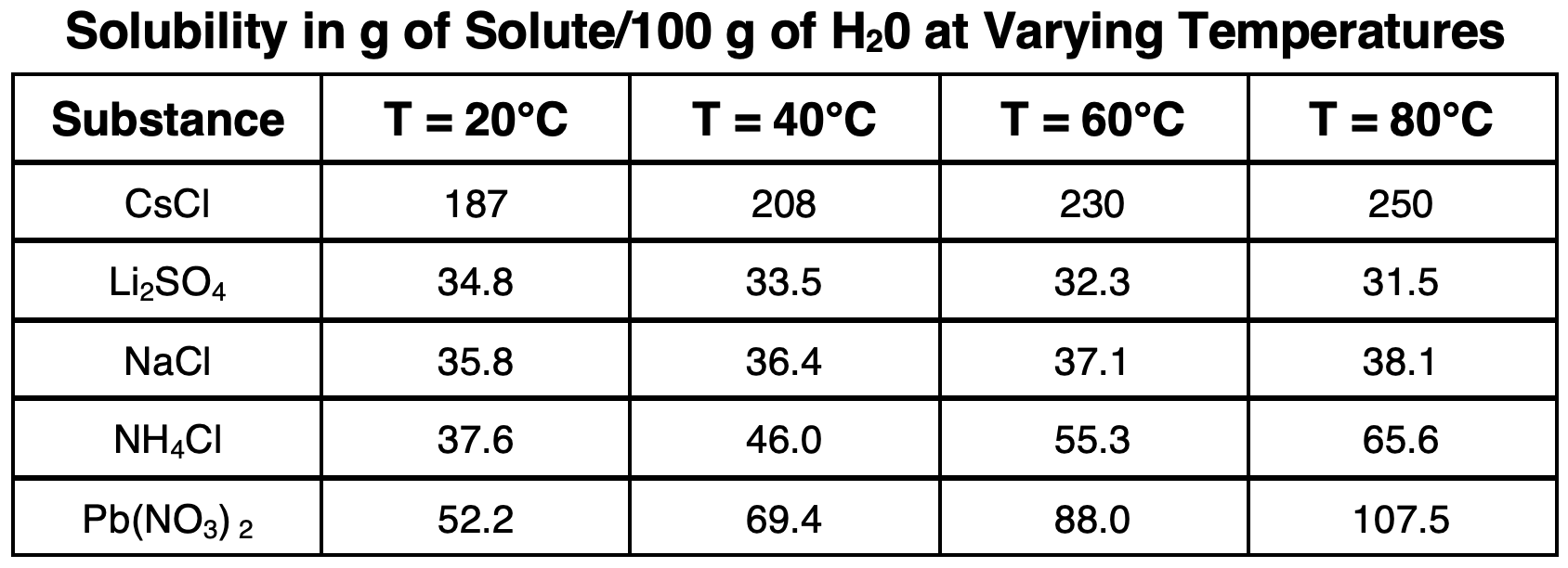
The graph below represents the solubility of varying ionic solids for a range of temperatures from 0°C to 100°C. Each line is referred to as a solubility curve. The units on solubility are grams of solute/100 g of water.
   
Observe how most lines on the graph slope or curve upward, indicating an increase in solubility with increasing temperature. Two substances - Li₂SO₄ and SO₂ slope downward. Sulfur dioxide is a gas and follows the usual trend for gases - decreasing solubility with increasing temperatures. Lithium sulfate (Li₂SO₄) is an ionic solid that is less soluble at higher temperatures. There are other salts (not shown) that follow the same trend as Li₂SO₄.
 
Let’s consider the ammonium chloride (NH₄Cl) line on the chart. At 30°C, approximately 40.0 g of NH₄Cl can dissolve in 100.0 g of water. This is the limit for solubility for this solute at this temperature. An NH₄Cl(aq) solution that contains 40.0 g NH₄Cl for every 100.0 g of H₂O is said to be a saturated solution. Additonal solute cannot be dissolved in the water at this temperature. If a NH₄Cl(aq) solution contains less than 40.0 g NH₄Cl for every 100.0 g of H₂O, then it is said to be an unsaturated solution.
 
Suppose that 50.0 g NH₄Cl were added to a 100.0 g of H₂O at 30.0°C and stirred. What would happen? Using the solubility of NH₄Cl from the solubility chart, we can predict that 40.0 g NH₄Cl will dissolve in the solution and the remaining 10.0 g NH₄Cl will remain undissolved. No amount of stirring or waiting or wishing will dissolve those additional 10.0 g NH₄Cl. The solution is satured with NH₄Cl once the 40.0 g NH₄Cl is dissolved.
 
Now suppose that 25.0 g NH₄Cl were added to a 100.0 g of H₂O at 30.0°C and stirred. What would happen? All the NH₄Cl would dissolve in the water. There would be no undissolved NH₄Cl present in the container. The solution would be unsaturated, meaning additional NH₄Cl could be added and dissolved. In fact, using the solubility of NH₄Cl from the chart, we can predict that an additional 15.0 g of NH₄Cl could be added and dissolved in the solution.
   
Solubility values are ratios - ratios of the mass of solute per mass of solvent (H₂O). The solution doesn’t always contain 100.0 g water, but the ratio of mass of solute per mass of solvent applies to all solutions regardless of the mass of solvent. Let’s consider an aqueous solution of NH₄Cl at 30.0 °C. The solubility of NH₄Cl is 40.0 g/100.0 g H₂O. What maximum amount of NH₄Cl can be dissolved into 50.0 g H₂O? What maximum amount of NH₄Cl can be dissolved into 200.0 g H₂O? For both questions, we can solve by using a ratio (or a conversion factor).
   
 
The following examples illustrate how the solubility curves can be used to make predictions. Use the Solubility Curves to determine the answers. Then check your answers.  

Example 1

Use the graph of solubility curves to determine if the following solutions would be saturated or unsaturated with solute under the given conditions.

1. A solution is made by adding 60.0 g of NaNO₃ to 100.0 g of H₂O at 20°C.
2. A solution is made by adding 100.0 g of NaNO₃ to 100.0 g of H₂O at 40°C.
3. A solution is made by adding 60.0 g of NaNO₃ to 50.0 g of H₂O at 20°C.
4. A solution is made by adding 100.0 g of NaNO₃ to 200.0 g of H₂O at 40°C.
5. A solution is made by adding 60.0 g of NaNO₃ to 50.0 g of H₂O at 60°C.

 
 

Answers and Explanations:

All five parts of this question involve the same solute (NaNO₃). Three different temperatures are involved. The solubility curve for NaNO₃ can be used to estimate the solubility at these three temperatures:

• At 20°C, solubility = ~86 g NaNO₃/100.0 g H₂O.
• At 40°C, solubility = ~100 g NaNO₃/100.0 g H₂O.
• At 60°C, solubility = ~120 g NaNO₃/100.0 g H₂O.

Now the information can be evaluated to answer Parts a-e. If the ratio of NaNO₃ to H₂O is less than the solubility, the solution is unsaturated. If the ratio is equal to the solubility, then the solution is saturated. And if the ratio is greater than the solubility, the solution is still saturated but there will be undissolved NaNO₃ remaining at the bottom of the container.
 
Answers:

1. Unsaturated (an additional 26 g NaNO₃ could be dissolved in the water)
2. Saturated
3. Saturated (with 17 g of undissolved NaNO₃ at the bottom of the container)
4. Unsaturated (200 g H₂O can hold up to 200 g NaNO₃ at this temperature)
5. Saturated (the ratio of NaNO₃ to H₂O is equivalent to the solubility of 120:100)

 
 
 

Example 2

For each situation below, use the graph of solubility curves to determine the maximum amount of solute that can be dissolved in the given amount of H₂O at the indicated temperature.

1. How much LiCl can be added to 100.0 g of water at 20°C?
2. How much LiCl can be added to 200.0 g of water at 20°C?
3. How much LiCl can be added to 100.0 g of water at 80°C?
4. How much NH₄Cl can be added to 100.0 g of water at 90°C?
5. How much NH₄Cl can be added to 50.0 g of water at 90°C?

 
Answers and Explanations:
The process will involve looking up the solubility for the given solute at the given temperature. Then use the solubility as part of a ratio to determine the amount of solute that must be added.
 

1. Solubility = ~80 g LiCl/100.0 g H₂O.  So, X/100.0 g H₂O = 80 g LiCl/100.0 g H₂O
   Solving for X, we get 80 g LiCl.
    
2. Solubility = ~80 g LiCl/100.0 g H₂O.  So, X/200.0 g H₂O = 80 g LiCl/100.0 g H₂O
   Solving for X, we get 160 g LiCl.
    
3. Solubility = 102 g LiCl/100.0 g H₂O.  So, X/100.0 g H₂O = 102 g LiCl/100.0 g H₂O
   Solving for X, we get 102 g LiCl.
    
4. Solubility = ~70 g NH₄Cl/100.0 g H₂O.  So, X/100.0 g H₂O = 70 g NH₄Cl/100.0 g H₂O
   Solving for X, we get 70 g NH₄Cl.
    
5. Solubility = ~70 g NH₄Cl/100.0 g H₂O.  So, X/50.0 g H₂O = 70 g NH₄Cl/100.0 g H₂O
   Solving for X, we get 35 g NH₄Cl.

 
 
 

Example 3

For the following descriptions of an unsaturated solution, use the graph of solubility curves to determine the amount of additional solute that can be added to the solution before it becomes saturated.

1. A solution is made at 30°C by adding 20.0 g of NaC₂H₃O₂ to 100.0 g of water. How much additional NaC₂H₃O₂ can be added before the solution is saturated?
2. A solution is made at 50°C by adding 40.0 g of NaC₂H₃O₂ to 100.0 g of water. How much additional NaC₂H₃O₂ can be added before the solution is saturated?
3. A solution is made at 50°C by adding 40.0 g of NaC₂H₃O₂ to 50.0 g of water. How much additional NaC₂H₃O₂ can be added before the solution is saturated?

 

Answers and Explanations:

The solution begins by determining the solubility for the given temperature. This will provide the ratio of NaC₂H₃O₂ to H₂O that is required for a saturated solution. From this, you can determine the total mass of NaC₂H₃O₂ that would be required for the given volume of H₂O. Then the additional mass that must be added to reach this total can be determined.
 

1. Solubility = ~50 g NaC₂H₃O₂/100.0 g H₂O.  Since the solution contains 100.0 g of H₂O, there will need to be a total of 50 g NaC₂H₃O₂ to saturate it. Thus, 30 g NaC₂H₃O₂ should be added to the 20.0 g that are already present.
    
2. Solubility = ~90 g NaC₂H₃O₂/100.0 g H₂O.  Since the solution contains 100.0 g of H₂O, there will need to be a total of 90 g NaC₂H₃O₂ to saturate it. Thus, 50 g NaC₂H₃O₂ should be added to the 40.0 g that are already present.
    
3. Solubility = ~90 g NaC₂H₃O₂/100.0 g H₂O.  Since the solution contains 50.0 g of H₂O (one-half of 100 g), there will need to be a total of 45 g NaC₂H₃O₂ (one-half of 90 g) to saturate it. Thus, 5 g NaC₂H₃O₂ should be added to the 40.0 g that are already present.

   
 

Supersaturated Solutions

From what has been said so far, it may be surprising to learn that a solution can be supersaturated. A supersaturated solution is a solution that contains more than the maximum amount of solute. A supersaturated solution cannot be made by simply adding more than the limit of how much solute the solvent can contain. Supersaturated solutions are made by taking advantage of the solubility-temperature relationship. For many salts, the solubility is greater at a higher temperature. A saturated solution at a high temperature will become a supersaturated solution when cooled down to a lower temperature. Let’s once again consider aqueous ammonium chloride - NH₄Cl(aq) - to illustrate the concept.
 
At 90°C, the solubility of NH₄Cl is 70.0 g per 100.0 g H₂O. Suppose we heated a beaker of 100.0 g of H₂O to a temperature of 90°C. Then we stirred in and dissolved 70.0 g of NH₄Cl to saturate it. Now suppose we left the beaker of saturated NH₄Cl(aq) on the lab bench and allowed it to cool down to a temperature of 30°C. What would happen? Nothing … other than the temperature changed by 60°C … and the solubility changed from 70 g/100.0 g H₂O. to 40.0 g/100.0 g H₂O. At 30°C, our beaker still contains 70.0 g NH₄Cl. But this is 30.0 g above the limit at the new temperature. The solution is a supersaturated solution.
   
The solubility curve below shows graphically how the supersaturated solution was made.

• Beginning at 90°C, a saturated solution was made by adding 70.0 g NH₄Cl to 100.0 g H₂O.
• The solution was then allowed to cool to 30°C where the solubility is less - 40.0 g NH₄Cl per 100.0 g H₂O.
• Because there was no change in the amount of solute or solvent in the beaker, the solution is now supersaturated, containing an extra 30.0 g of NH₄Cl(aq).

   
A supersaturated solution is not a stable solution. It is a solution that is bloated with dissolved solute that is ready to drop out of the solution. The dissolved ions are surrounded by water, postponing their ability to attract and form a crystalline precipitate. To initialize precipitation of the extra, above-the-limit solute, a crystal of the solid can be dropped into the solution. The crystal provides a site about which precipitation can occur. Solvated ions escape and attach to the crystal. Precipitation rapidly accelerates and spreads through the entire container. Bumping or disturbing the container can also cause the excess solute to precipitate.
 
Photo Source: Wikimedia Commons
 
 
 

Example 4

A beaker containing 100.0 g of H₂O is heated to 80°C. Sodium acetate (NaC₂H₃O₂) is then dissolved into the solution to saturate it.

1. How many grams of NaC₂H₃O₂ should be added to the 100.0 g of H₂O to saturate the solution?
2. Once the solution is made, it is set aside to cool to 30°C. How many grams of NaC₂H₃O₂ are present in the solution once it has cooled to 30°C?
3. What is the solubility of NaC₂H₃O₂ at 30°C? Is the solution unsaturated, saturated, or supersaturated?
4. Describe what will happen if a small crystal of NaC₂H₃O₂ is added to the solution. Be quantitative in your description.

 

Answers and Explanations:

1. At 80°C, the solubility is ~150 g NaC₂H₃O₂/100.0 g H₂O. Add and dissolve 150 g NaC₂H₃O₂ in the water.
    
2. There will still be 150 g NaC₂H₃O₂ dissolved in the water. Cooling the solution does not change the amount of solute or solvent present.
    
3. At 30°C, the solubility is ~50 g NaC₂H₃O₂/100.0 g H₂O. The solution is supersaturated since it contains more than 50 g of NaC₂H₃O₂.
    
4. A supersaturated solution is unstable and will precipitate some of the excess solute when a crystal is added. So, adding the crystal will cause 100.0 g NaC₂H₃O₂ to precipitate. This will leave 50.0 g NaC₂H₃O₂ dissolved in the 100.0 g of H₂O.

 
 
 
 
 
 

Effect of Temperature on Gas Solubility

Unlike many solids, the solubility of gases in water are less at higher temperature. The inverse relationship between gas solubility and temperature is shown in the graph below.
   
Like solids, a gas particle must be attracted and surrounded by water molecules to become part of the aqueous solution. At higher temperatures, gas particles that have entered the water are moving faster and are more difficult to surround. At higher temperatures, they are more likely to escape the liquid before being surrounded by water.
 
 
 

Effect of Pressure on Gas Solubility

A final factor that affects the solubility of a gas in water is the pressure of the gas above the solution. At higher pressures, the concentration of gas particles in the space above the water increases. This increases the frequency at which gas particles collide with the water surface. Increases in those collisions provides more opportunities for water molecules to attract, surround, and stabilize the gas particles in the aqueous state.
   
In 1803, English chemist William Henry proposed an equation relating the solubility of a gas in a solvent to the pressure of the gas above the solvent. Henry proposed that the concentration of a gaseous solute dissolved in a liquid solvent is proportional to the pressure of the gas above the solvent. His equation, now known as Henry’s Law, is
 
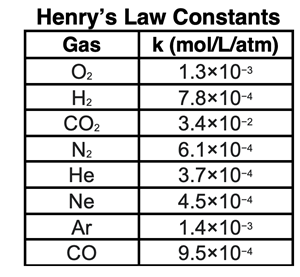
where C is the concentration of the solute in the solution, P is the pressure of the gas above the solution, and k is a constant of proportionality that depends upon the identities of the solute and the solvent. Values of k, referred to as Henry’s Law constants, are determined experimentally. The table at the right shows a sampling of k values for a variety of gases dissolving in water at a temperature of 25°C.
 
 
 
 
 

Example 5

Determine the concentration of CO₂ gas at 25°C in mol/L and g/L in an aqueous solution at a pressure of …

1. 1.0 atm.
2. 2.0 atm.
3. 4.0 atm.
4. 10.0 atm.

 

Solution:

Henry’s Law constant (k) for CO₂ in water is 3.4x10^-2 mol/L/atm or 0.034 mol/L/atm. The concentration in mol/L can be calculated for the Part a - d pressures using the equation C = k•P. Once determined in mol/L, the molar mass of CO₂ (44.01 g/mol) can be used to determine the concentration in g/L. The two-part answers for a.-d. are shown below:
   
 
 

Before You Leave

• Download our Study Card on Solubility, Temperature, and Pressure. Save it to a safe location and use it as a review tool. (Coming Soon)
• Our Calculator Pad section is the go-to location to practice solving problems. Here’s two good follow-ups to this lesson: Problem Set MS1: Solubility Curves 1 and Problem Set MS2: Solubility Curves 2.
• The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.

 
 
 
 

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
1. Identify the following statements as being True or False. If False, correct the statement or explain what is wrong with it.

1. A large lattice energy is likely to cause a dissolving process a exothermic process. 
   
   Check Answer
   Answer: FALSE
   
   Lattice energies are related to pulling ions of a salt away from its lattice. It is the endothermic step of dissolving a salt. If the lattice energy is large, the dissolving process is more likely to be endothermic.
   
    
   
    
2. All ionic solids are soluble in water. 
   
   Check Answer
   Answer: FALSE
   
   Many are. But some ionic solids are insoluble in water ... like AgCl, BaSO₄, Pb(C₂H₃O₂)₂, and many more.
   
    
   
    
3. Increasing temperature always increases the solubility of a salt in water. 
   
   Check Answer
   Answer: FALSE
   
   It often does. But it definitely isn't a guarantee. There are numerous salts whose solubility decreases with temperature. Li₂SO₄ is one of them, as shown on the solubility chart.
   
    
   
    
4. Increasing temperature always decreases the solubility of a gas in water. 
   
   Check Answer
   Answer: TRUE
   
    
   
    
5. If a salt has a solubility of 20 g/100 g H₂O at a temperature of 25°C, then a supersaturated solution can be made by adding 30 g of solute to 100 g H₂O at 25°C. 
   
   Check Answer
   Answer: FALSE
   
   To make a supersaturated solution, you must take advantage of the solubility-temperature relationship. For instance, warm the water and dissolve enough solute in it to create a saturated solution at high temperature. Then allow the solution to cool down towards room temperature. The solution will now contain more solute than it should at the lower temperature and is considered supersaturated.
   
    
   
    
6. Increasing the pressure of a gas above a liquid solvent will cause more gas to be dissolved in that solvent. 
   
   Check Answer
   Answer: TRUE
   
   Yes! This is Henry's Law. And we take advantage of it by bottling carbonated drinks at high pressure. This causes a greater solubility and more CO₂ to be dissolved in the solution. That's happy news for the taste buds and terrible news for the teeth. As such, it doesn't quite qualify for a Chemistry for Better Living award.
   
    
   
    

 
 
2. Consider the solubility curves for solutes X, Y, and Z in water.
   

1. Determine the solubility of substance X at 20°C. 
   
   Check Answer
   Answer: ~110 g X/100 g H₂O
   
    
   
    
2. Determine the solubility of substance Y at 40°C. 
   
   Check Answer
   Answer: ~96 g Y/100 g H₂O
   
    
   
    
3. Determine the solubility of substance Z at 60°C. 
   
   Check Answer
   Answer: ~84 g Z/100 g H₂O
   
    
   
    
4. Approximately how many times more soluble is substance X than substance Y at 20°C? 
   
   Check Answer
   Answer: ~1.57 times greater solubility
   
   At 20°C: the solubilities are
   X: ~110 g X/100 g H₂O
   Y: ~70 g Y/100 g H₂O
   Dividing the value for X by the value of Y will indicate how many times more soluble X is than Y:
   110/70 = 1.57
   
    
   
    
5. Approximately how many times more soluble is substance X than substance Z at 50°C? 
   
   Check Answer
   Answer: ~1.63 times greater solubility
   
   At 50°C: the solubilities are
   X: ~122 g X/100 g H₂O
   Y: ~75 g Y/100 g H₂O
   Dividing the value for X by the value of Y will indicate how many times more soluble X is than Y:
   122/75 = 1.63
   
    
   
    

 
 
3. Consider the solubility curves for solutes X, Y, and Z in water.
   

1. How many g of X can be dissolved in 100 g H₂O at 50°C? 
   
   Check Answer
   Answer: 122 g X
   
   From the graph, the solubility is 122 g X/100 g H₂O. So if there are 100 g of H₂O, there can be 122 g X dissolved into it. 
   
    
   
    
2. How many g of X can be dissolved in 50 g H₂O at 50°C? 
   
   Check Answer
   Answer: 61 g X
   
   From the graph, the solubility is 122 g X/100 g H₂O. So if there are 50 g of H₂O (one-half the solvent), there can be 61 g X (one half as much X) dissolved into it. 
   
    
   
    
3. How many g of X can be dissolved in 200 g H₂O at 50°C? 
   
   Check Answer
   Answer: 244 g X
   
   From the graph, the solubility is 122 g X/100 g H₂O. So if there are 200 g of H₂O (twice as much solvent), there can be 244 g X (twice as much X) dissolved into it. 
   
    
   
    
4. How many g of Y can be dissolved in 100 g H₂O at 70°C? 
   
   Check Answer
   Answer: 140 g Y
   
   From the graph, the solubility is 140 g Y/100 g H₂O. So if there are 100 g of H₂O, there can be 140 g Y dissolved into it. 
   
    
   
    
5. How many g of Y can be dissolved in 80 g H₂O at 70°C? 
   
   Check Answer
   Answer: 112 g X
   
   From the graph, the solubility is 140 g Y/100 g H₂O. So if there are 80 g of H₂O (four-fifths the solvent), there can be 61 g Y (four-fifths as much Y) dissolved into it. 
   
   Set up a solute-to-solvent ratio like ... Y/80 = 140/100 ... and solve for Y.
   
    
   
    
6. An aqueous solution of Z contains 20 g of Z in 100 g of H₂O at 40°C. What additional mass of Z must be added to the water for the solution to be saturated? 
   
   Check Answer
   Answer: An additional 46 g Z
   
   From the graph, the solubility is 66 g Z/100 g H₂O. So if there are 100 g of H₂O, there can be 66 g Z dissolved into it. Since 20 g have already been dissolved into the water, an addition 46 g can be added and stirred in for a total of 66 g of Z.
   
    
   
    
7. An aqueous solution of Z contains 20 g of Z in 50 g of H₂O at 80°C. What additional mass of Z must be added to the water for the solution to be saturated? 
   
   Check Answer
   Answer: An additional 31 g Z
   
   From the graph, the solubility is 102 g Z/100 g H₂O. So if there are 50 g of H₂O (one-half the solvent), there can be 51 g Z (one-half the solute) dissolved into it. Since 20 g have already been dissolved into the water, an addition 31 g can be added and stirred in for a total of 51 g of Z.
   
    
   
    
8. Noah Formula adds 120 g of Y to 100 g H₂O at 50°C and stirs for several minutes. What type of solution is formed - unsaturated, saturated, supersaturated? Is there any undissolved Y remaining in the beaker? If so, then how much? 
   
   Check Answer
   Answer: Saturated, with 8 g of undissolved Y in the beaker
   
   At 50°C, the solubility of Y is 112 g Y/100 g H₂O. So if Noah adds 120 g Y to 100 g H₂O, only 112 g of the Y will dissolve since that is the limit. The solution will be saturated but there will be undissolved solid at the bottom of the container. This will consist of 8 g of undissolved Y.
   
    
   
    

 
 
4. Anna Litical is attempting to create a supersaturated solution of Y (referring to above graph). She starts with a beaker of 100.0 g of H₂O at 90°C. Describe the steps she must perform to  create a supersaturated solution of Y at 20°C.