Lesson 2: Acid-Base Equilibria

Part c: Dissociation of Polyprotic Acids

Part a: Weak Acid and Weak Base Dissociation
Part b: Percent Dissociation and K_a and K_b
Part c: Dissociation of Polyprotic Acids
Part d: Determination of the pH of Salts
Part e: Common Ion Effects and Buffers
Part f: Titration Analysis

 

The Big Idea

From diprotic to triprotic acids, understanding the sequential dissociation process helps students master equilibrium concepts and acid strength comparisons.

 

 

What are Polyprotic Acids?

Polyprotic acids are acids that contain two or more ionizable protons. A monoprotic acid like HCl or HNO₃ or HF has a single ionizable proton. But a diprotic acid like H₂SO₄ or H₂CO₃ has two ionizable protons and a triprotic acid like H₃PO₄ or H₃C₆H₅O₇ has three ionizable protons. The list at the right displays the formulae of several diprotic and triprotic acids.
 
Like any acid, polyprotic acids are proton donors. They can be modeled as dissociating in a stepwise fashion. In pure water, the first proton is donated to water to form a hydronium ion (H₃O⁺) and the conjugate base of the acid. For instance, carbonic acid (H₂CO₃) dissociates to form the hydrogen carbonate ion (HCO₃^-).

H₂CO₃(aq)  +  H₂O(l)    ⇄    H₃O⁺(aq)   +  HCO₃^-(aq)

The HCO₃^- ion is amphiprotic. That is, it can act as both a proton donor and a proton acceptor. When it acts as an acid, it donates a proton to water to form the hydronium ion (H₃O⁺) and its conjugate base (CO₃^2-).

HCO₃^-(aq)  +  H₂O(l)    ⇄    H₃O⁺(aq)   +  CO₃^2-(aq)

Both steps produced hydronium ions and can affect the pH of the solution.
 
 
 

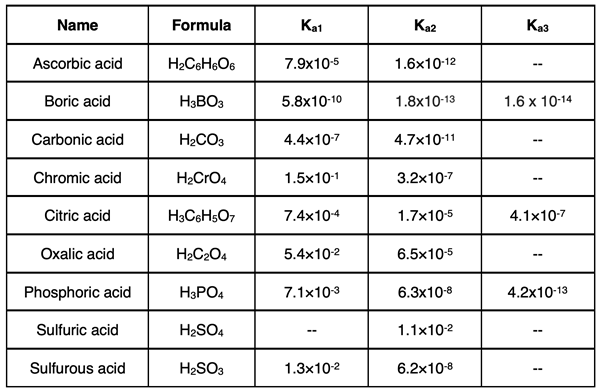
Dissociation Constants of Polyprotic Acids

Each dissociation step of a polyprotic acid has its own dissociation constant. These dissociation constants are distinguished from one another by the symbols K_a1, K_a2, and K_a3. These K_a values are usually much less than 1, indicating a very weak forward reaction and an equilibrium that lies on the reactant side. This means the polyprotic acids are weak acids. The lone exception is sulfuric acid, H₂SO₄. The first dissociation step for H₂SO₄ has a K_a1 value much greater than 1. Thus, H₂SO₄ dissociates as a strong acid to form the HSO₄^- ion. The K_a2 value for the second dissociation step is less than 1. So, the HSO₄^- ion dissociates as a weak acid.

H₂SO₄(aq)  +  H₂O(l)     →    H₃O⁺(aq)   +  HSO₄^-(aq)        Strong Acid
 
HSO₄^-(aq)  +  H₂O(l)    ⇄    H₃O⁺(aq)   +  SO₄^2-(aq)        K_a2 = 1.1x10^-2

 

Each dissociation step of any polyprotic acid contributes to the overall concentration of H₃O⁺, and thus the pH. However, they do not contribute equally to the concentration of H₃O⁺. The first dissociation step makes the greatest contribution to [H₃O⁺]. The second step makes a very small and often negligible contribution to the [H₃O⁺]. For triprotic acids, the third dissociation step makes a negligible contribution to the [H₃O⁺]. The ability of the second step to contribute to the overall [H₃O⁺] is dependent upon how close the K_a2 value is to the K_a1 value.
 
Dissociation constants for several diprotic and triprotic acids are shown in the table below. Additional K_a values can be found in the Reference section of our Chemistry Tutorial.

 
 

 
 
 

Determining the pH of Polyprotic Acids

Our discussion of methods for weak acid dissociation problems has involved a relatively strict adherence to several steps. These steps include writing a dissociation equation, writing a K_a equation, setting up an ICE table, and substituting expressions and/or values from the Equilibrium row of the ICE table into the K_a equation.
 
Our analyses below for polyprotic acids assume some comfort on the part of the reader with the simpler monoprotic acid dissociation. We recommend an earlier page from this Chapter – Weak Acid and Weak Base Dissociation – to those who have not yet attained such a comfort.
 
The mathematics of K_a problems are simplified by using the 5-Percent Rule. The rule assumes that the contribution of a weak acid’s dissociation to the equilibrium concentration of the weak acid is negligible as long as less than five percent of it dissociates. The rule allows us to make approximations like

2.5 -x   ≈  2.5

The 5-Percent Rule states that the assumption is valid as long as value of x is less than 5% of 2.5. Once the problem is solved, we check the value of x to ensure that it satisfies the 5-Percent Rule.
 
 
 

Carbonic Acid, H₂CO₃

Let’s begin our analyses by determining the pH of a 1.0 M solution of carbonic acid (H₂CO₃). The balanced equation for the first dissociation step and the corresponding K_a1 value is listed below.

H₂CO₃(aq)  +  H₂O(l)    ⇄    H₃O⁺(aq)   +  HCO₃^-(aq)        K_a1 = 4.4x10^-7

The dissociation constant equation relates the K_a1 value to equilibrium concentrations of the acid and its ions:

K_a1 = [H₃O⁺] • [HCO₃^-] / [H₂CO₃]

 

An ICE table is used to relate the initial acid concentration (1.0 M) to the equilibrium concentrations. Notice how we have applied the 5-Percent Rule in the bottom row of the table (1.0 – x  ≈ 1.0).

 
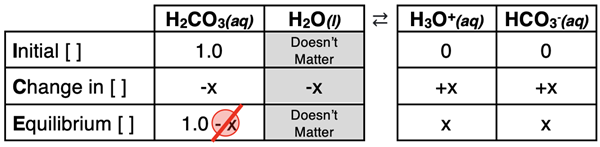
The expressions in the Equilibrium row and the K_a1 value can be substituted into the dissociation constant equation in order to solve for x. The algebra is as follows.

K_a1 = [H₃O⁺] • [HCO₃^-] / [H₂CO₃]
 
4.4x10^-7 = x • x / 1.0
 
4.4x10^-7 = x²
 
x = √ (4.4x10^-7)
 
x = 6.63325x10^-4

 

Since x is less than 5% of 1.0, the assumption that 1.0 – x  ≈ 1.0 was valid. The value of x indicates the contribution of the first dissociation step to the equilibrium concentrations of H₃O⁺ and HCO₃^-. The second step may or may not contribute to these values. We will now perform the math to see if it does.
 
The second dissociation step and its corresponding K_a2 value are shown below.

HCO₃^-(aq)  +  H₂O(l)    ⇄    H₃O⁺(aq)   +  CO₃^2-(aq)        K_a2 = 4.7x10^-11

The equilibrium constant equation for this step is:

K_a2 = [H₃O⁺] • [CO₃^2-] / [HCO₃^-]

 

The ICE table for the second step is shown below. Note that the initial concentrations of H₃O⁺ and HCO₃^- are the values that resulted from the first dissociation step. The reaction must proceed to the right to reach equilibrium since there is initially no CO₃^2- ions to push the reaction to the left. Thus, y is subtracted from reactants and added to products in the Change row of the table. Note that in the Equilibrium row, the 5-Percent Rule is assumed for both H₃O⁺ and HCO₃^- ions.

 
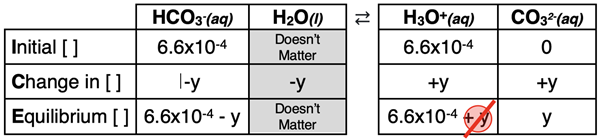
Once again, the expressions in the Equilibrium row and the K_a2 value can be substituted into the dissociation constant equation in order to solve for y. The algebra is as follows.

K_a2 = [H₃O⁺] • [CO₃^2-] / [HCO₃^-]
 
4.7x10^-11 = (6.6x10^-4) • y / (6.6x10^-4)
 
4.7x10^-11 = (6.6x10^-4) • y / (6.6x10^-4)
 
y = 4.7x10^-11

 

The value of y is much less than 5% of 6.6x10^-4. Thus, the assumptions that 6.6x10^-4 - y ≈ 6.6x10^-4 and 6.6x10^-4 + y ≈ 6.6x10^-4 are valid. We can now determine the equilibrium concentration of H₃O⁺ and the pH as ...

[H₃O⁺] = 6.6x10^-4 + y =  6.6x10^-4 + 4.7x10^-11 = 6.6x10^-4 M
 
pH = -log(6.6x10^-4) = 3.18

As can be seen in the above math, the second dissociation step makes a negligible contribution to the pH of the solution.

 
 

 
 
 

Phosphoric Acid, H₃PO₄

Phosphoric acid is a triprotic acid. There are three dissociation steps. We will conduct an analysis to determine the pH of a 5.0 M solution of phosphoric acid (H₃PO₄). While there are three dissociation steps, the second and the third step may make a negligible contribution to the concentration of H₃O⁺ and the pH of the solution.
 
The balanced equation for the first dissociation step and the corresponding K_a1 value is listed below.

H₃PO₄(aq)  +  H₂O(l)    ⇄    H₃O⁺(aq)   +  H₂PO₄^-(aq)        K_a1 = 7.1x10^-3

The dissociation constant equation relates the K_a1 value to equilibrium concentrations of the acid and its ions:

K_a1 = [H₃O⁺] • [H₂PO₄^-] / [H₃PO₄]

 

An ICE table is used to relate the initial acid concentration (5.0 M) to the equilibrium concentrations. Notice how we have applied the 5-Percent Rule in the bottom row of the table (5.0 – x  ≈ 5.0).

 
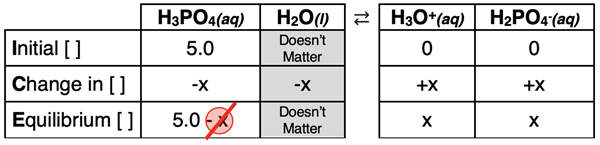
The expressions in the Equilibrium row and the K_a1 value can be substituted into the dissociation constant equation in order to solve for x. The algebra is as follows.

K_a1 = [H₃O⁺] • [H₂PO₄^-] / [H₃PO₄]
 
7.1x10^-3 = x • x / 5.0
 
(5.0)•(7.1x10^-3) = x²
 
x = √ (3.55x10^-2)
 
x = 0.1884144 ...

Since x is less than 5% of 5.0, we can assume are assumption that 5.0 – x  ≈ 5.0 was valid. The value of x indicates the contribution of the first dissociation step to the equilibrium concentrations of H₃O⁺ and H₂PO₄^-. The second step may or may not contribute to these values. We will now perform the math to see if it does.
 
The second dissociation step and its corresponding K_a2 value are shown below.

H₂PO₄^-(aq)  +  H₂O(l)    ⇄    H₃O⁺(aq)   +  HPO₄^2-(aq)        K_a2 = 6.3x10^-8

 

The equilibrium constant equation for this step is:

K_a2 = [H₃O⁺] • [HPO₄^2-] / [H₂PO₄^-]

 

The ICE table for the second step is shown below. The initial concentrations of H₃O⁺ and H₂PO₄^- are the values that resulted from the first dissociation step. The reaction proceeds to the right to reach equilibrium; thus, y is subtracted from reactants and added to products in the Change row of the table. Note that in the Equilibrium row, the 5-Percent Rule is assumed for both H₃O⁺ and HPO₄^2- ions.

 
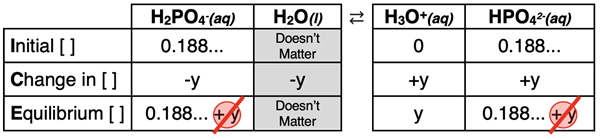
The expressions in the Equilibrium row and the K_a2 value can be substituted into the dissociation constant equation in order to solve for y. The algebra is as follows.

K_a2 = [H₃O⁺] • [HPO₄^2-] / [H₂PO₄^-]
 
6.3x10^-8 = (0.188 ...) • y / (0.188 ...)
 
6.3x10^-8 = (0.188 ...) • y / (0.188 ...)
 
y = 6.3x10^-8

 

The value of y is much less than 5% of 0.188 ... . Thus, the assumptions that 0.188 - y ≈ 0.188 and 0.188 + y ≈ 0.188 are valid. Since the second dissociation step has made a negligible contribution to the [H₃O⁺] and pH, we can also neglect the contribution of the third dissociation step. We can now determine the equilibrium concentration of H₃O⁺ and the pH as ...

[H₃O⁺]  =  0.1884144 ... + y =  0.1884144 ...  +  6.3x10^-8  =  0.1884144 ... M
 
pH = -log(0.1884144 ...) = 0.72

 

The value of K_a1 for H₃PO₄ is on the larger side for a weak acid. Because of its relatively large size, the percent dissociation is sometimes greater than 5% for a more diluted [H₃PO₄]. When this occurs, the 5-Percent Rule is not a valid assumption and the mathematics becomes more complicated.  A 1.0 M solution of H₃PO₄ is more than 5% dissociated. Once that is determined the mathematics must be re-worked as follows:

K_a1 = [H₃O⁺] • [H₂PO₄^-] / [H₃PO₄]
 
7.1x10^-3 = x • x / (1.0 - x)
 
(1.0 - x)•(7.1x10^-3) = x²
 
  -  7.1x10^-3•x  = x²
 
0  =  x²  +  7.1x10^-3•x  -  7.1x10^-3

This results in a quadratic equation and the value of x must be found using the quadratic formula.
 

 

 
 

Sulfuric Acid, H₂SO₄

Our last analysis will involve the determination of the pH of a 0.25 M solution of sulfuric acid, H₂SO₄. As mentioned earlier, the first dissociation step is a complete dissociation.

H₂SO₄(aq)  +  H₂O(l)     →    H₃O⁺(aq)   +  HSO₄^-(aq)        Strong Acid

The concentrations of H₃O⁺ and HSO₄^- will be equal to 0.25 M.
 
The second dissociation step is a reversible reaction with an equilibrium that lies to the left.

HSO₄^-(aq)  +  H₂O(l)    ⇄    H₃O⁺(aq)   +  SO₄^2-(aq)        K_a2 = 1.1x10^-2

The K_a2 value is relatively large for a weak acid dissociation which means that there will be more than 5% dissociation for certain concentrations of H₂SO₄.
 
The equilibrium constant equation for the second step is:

K_a2 = [H₃O⁺] • [SO₄^2-] / [HSO₄^-]

 

The ICE table is shown below. We have assumed the Five-Percent Rule and will check later to see if it is valid.

 
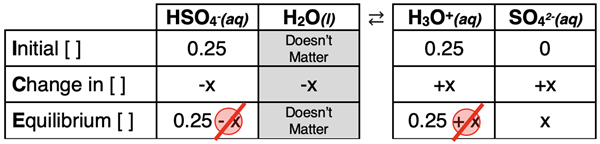
The expressions in the Equilibrium row and the K_a2 value can be substituted into the dissociation constant equation in order to solve for x. The algebra is as follows.

K_a2 = [H₃O⁺] • [SO₄^2-] / [HSO₄^-]
 
1.1x10^-2 = (0.25) • x / (0.25)
 
x = 1.1x10^-2

The value of x is 4.4% of the 0.25. The Five-Percent Rule is just barely valid.
 
We can now calculate the equilibrium concentration of H₃O⁺ and the pH as ...

[H₃O⁺]  =  0.25 + x =  0.25  +  0.011  =  0.261 M
 
pH = -log(0.261) = 0.58
 

 
 

Before You Leave - Practice and Reinforcement

Now that you've done the reading, take some time to strengthen your understanding and to put the ideas into practice. Here's some suggestions.

• Our Calculator Pad section is the go-to location to practice solving problems. You’ll find plenty of practice problems on our Solution Equilibria page. Check out the following problem set:  Set SAB9: Polyprotic Acids
• The Check Your Understanding section below includes questions with answers and explanations. It provides a great chance to self-assess your understanding.
• Download our Study Card on Polyprotic Acid Dissociation. Save it to a safe location and use it as a review tool.

 
 
 

Check Your Understanding of Polyprotic Acids

Use the following questions to assess your understanding of how to analyze the dissociation of a polyprotic acid. Tap the Check Answer buttons when ready.
 
1. Use the dissociation constants in the table above to determine the pH of a 0.50 M solution of ascorbic acid (H₂C₆H₆O₆).
 

 
2. Use the dissociation constants in the table above to determine the pH of a 1.5 M solution of boric acid (H₃BO₃).
 







​