Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Lesson 2: Acid-Base Equilibria
Part e: Titration Analysis
Part a:
Weak Acid and Weak Base Dissociation
Part b:
Percent Dissociation and Ka and Kb
Part c:
Dissociation of Polyprotic Acids
Part d:
Determination of the pH of Salts
Part e:
Common Ion Effects and Buffers
Part f: Titration Analysis
The Big Idea
A titration curve is not just a shape—it’s a story of acid, base, and equilibrium. In this lesson, we’ll break down how to compute the pH at key points (before, at, and after equivalence) in a weak-acid/strong-base titration.
Titration Curves
The topic of titration was introduced in Chapter 15 of this Chemistry Tutorial. A titration is an analytical procedure that is used to determine the moles of acid (or base) in a sample of unknown concentration. On this page, we will revisit the topic of titration with a focus on explaining the mathematics of pH curves (sometimes called titration curves). We will restrict our discussion to the titration of a weak acid with a strong base.
As the known solution (referred to as the titrant) is added to the unknown solution (the analyte), the acid and base react and the pH naturally undergoes a change. As the equivalence point is approached, there is a sudden and steep increase in the pH of the solution. Once the equivalence point has been passed, the pH begins to level off. This pattern of pH change is clearly seen in a pH curve (or titration curve). We have previously discussed the conceptual aspect of these titration curves. We now wish to show the mathematical basis for these patterns of change.
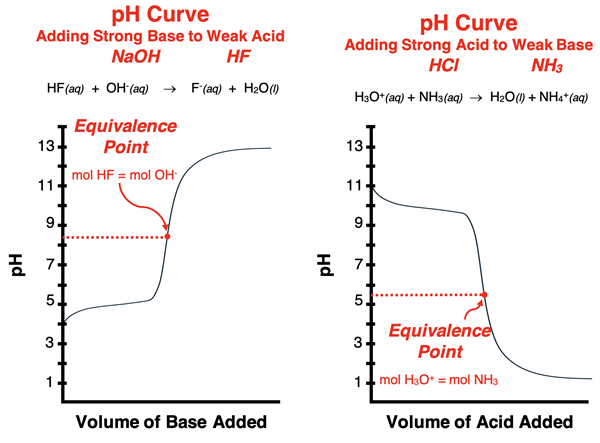
Titration of a Weak Acid with a Strong Base - Before the Equivalence Point
Here are the conditions: we have a generic weak acid, HA, with a Ka value of 1.0x10-5. We will titrate 40.0 mL of a 1.00 M solution of HA with a 2.00 M solution of the strong base NaOH. We will conduct a pH analysis for several points during the titration for varying volumes of NaOH being added to the weak acid.
Given these conditions, we can predict that the equivalence point occurs when 20.0 mL of NaOH have been added to the flask.
Vbase = Macid •Vacid / Mbase
Vbase = (1.00 M) • (0.0400 L) / (2.00 M)
Vbase = 0.0200 L = 20.0 mL
We can also determine the moles of acid initially present as ...
Moles HA = 0.0400 L • (1.00 mol HA / 1 L) = 0.0400 mol HA
As the strong base (NaOH) is added to the 0.0400 moles of weak acid, a neutralization reaction occurs as a proton is transferred from the HA to the base.
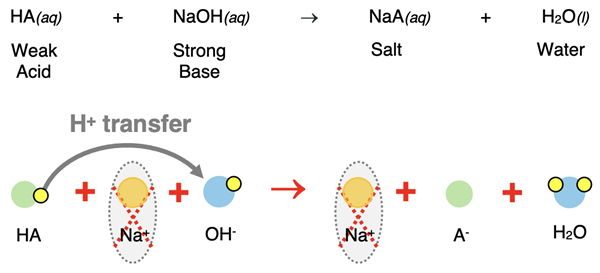
Before the equivalence point is reached, the acid will be in excess and the added base will completely react. We can use the amount of NaOH added to determine the moles of A- produced. The excess acid (HA) and its conjugate base will be present in solution; the pH can be calculated from their concentrations.
Example 1: 10.0 mL of 2.00 M NaOH added to 40.0 mL of 1.00 M HA
It was mentioned that the equivalence point occurs when 20.0 mL of NaOH is added. When 10.0 mL are added, the titration is half-way to the equivalence point. The table below shows one-half the original HA being neutralized.
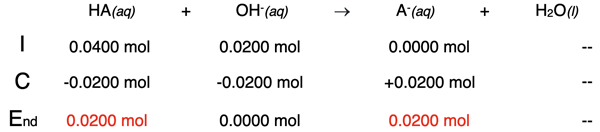
This leaves 0.0200 moles of HA in solution with the 0.0200 moles of A- that have been produced. Their concentrations can be determined by dividing the moles by the total volume in liters - at this point, 40.0 mL + 10.0 mL.
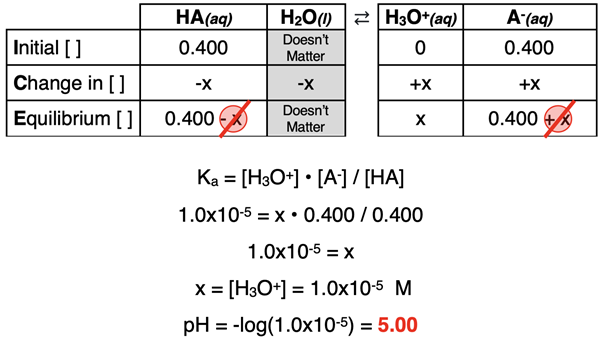
[HA] = 0.0200 mol / 0.0500 L = 0.400 M
[A-] = 0.0200 mol / 0.0500 L = 0.400 M
We can now calculate the pH of this solution, knowing that we have a weak acid with its conjugate base. We treat this as a common ion problem. The ICE table and mathematics is shown. (If necessary, review our Common Ion Effect page.)
Example 2: 19.0 mL of 2.00 M NaOH added to 40.0 mL of 1.00 M HA
Our second calculation will be for a point just prior to the equivalence point. After adding 19.0 mL of NaOH (a mere 1.0 mL short of the equivalence point), the number of moles of NaOH is:
Moles NaOH = 0.0190 L • (2.00 mol NaOH / 1 L) = 0.0380 mol NaOH
This base will react away and neutralize 0.0380 moles of HA, forming an equal amount of A- ions. This is stoichiometry. The results are shown in the table below:
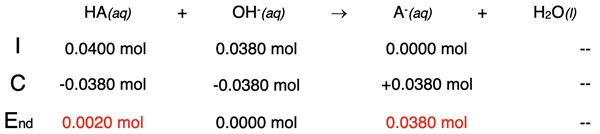
This leaves 0.0020 moles of HA in solution with the 0.0200 moles of A- that have been produced. Their concentrations can be determined by dividing the moles by the total volume in liters - at this point, 40.0 mL + 19.0 mL.
[HA] = 0.0020 mol / 0.0590 L = 0.03389 ... M
[A-] = 0.0380 mol / 0.0590 L = 0.64406 ... M
We can now calculate the pH of this solution, knowing that we have a weak acid with its conjugate base. We treat this as a common ion problem. The ICE table and mathematics is shown.
Summary - Before the Equivalence Point
The calculations shown in Examples 1 and 2 involved first determining what species were present and the concentrations of those species after the neutralization reaction between the weak acid and the NaOH. Before the equivalence point, the species were the weak acid HA and its conjugate base. Then an ICE table was used to determine the pH of this common ion situation.
Results of additional calculations are shown below.
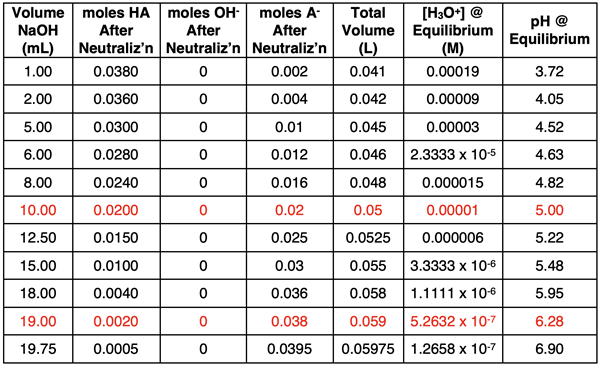
If data from a spreadsheet for NaOH volumes from 0.00 mL to 19.75 mL in 0.25-mL increments are plotted, the results would look like the graph at the right. It’s beginning to look like a titration curve. It’s now time to analyze the equivalence point.
Example 3: 20.0 mL of 2.00 M NaOH added to 40.0 mL of 1.00 M HA
At the equivalence point, the moles of NaOH added to the flask will be equal to the moles of HA. The weak acid will be entirely neutralized and no longer remaining in the flask. This will occur when 20.0 mL of NaOH are added. The table depicts this situation.
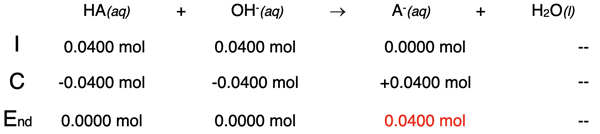
The only species remaining after neutralization is the A-.
[A-] = 0.0400 mol / 0.0600 L = 0.6666 ... M
The A- is the conjugate base of a weak acid. It will undergo hydrolysis to produce HA and OH-. We learned in Lesson 2c how to determine the pH of such a solution. The ICE table and accompanying mathematics is shown below. (If necessary, review our Hydrolysis of Salts page.)
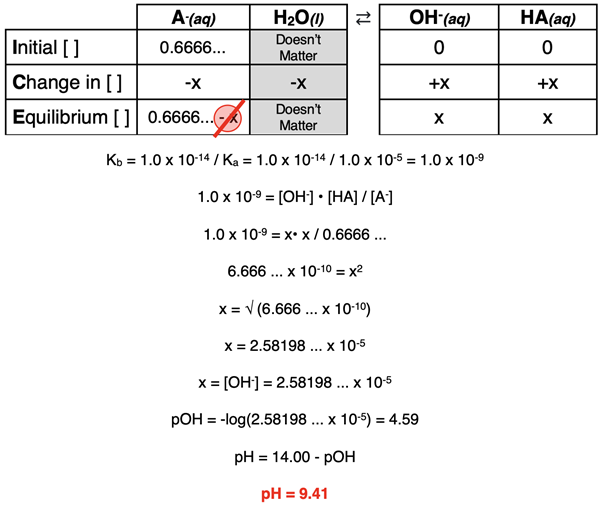
Summary - At the Equivalence Point
At the equivalence point, the dominant species present in solution after the neutralization is the conjugate base of the weak acid. Since it is a base, the pH will be greater than 7.0 at the equivalence point. The actual value can be calculated by analyzing the hydrolysis of the base with water. This requires that a Kb value be determined for its hydrolysis and an ICE table be used.
The titration curve at the right depicts our most recent calculation. It is now time to analyze the pH for volumes that exceed that of the equivalence point.
Example 4: 21.0 mL of 2.00 M NaOH added to 40.0 mL of 1.00 M HA
The equivalence point occurs when 20.0 mL of NaOH are added to the flask. The addition of 21.0 mL is a mere 1.0 mL past the equivalence point. The stoichiometry of the neutralization must first be analyzed. This is shown in the table below.
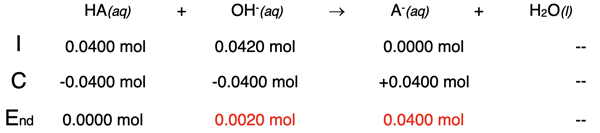
Once the base neutralizes the acid, there will be excess of 0.0020 mol of the base (OH-). There will also be A- ions in the solution; this is the conjugate base of a weak acid. Of these two species - OH- and A- - the OH- is a much stronger base. It is a strong base compared to A- which is a weak base. So, the pH of the solution will be based on the presence of hydroxide ions. The molarity can be calculated by dividing the number of moles by the total volume - 40.0 mL + 21.0 mL
[OH-] = 0.0020 mol / 0.0610 L = 0.03278 ... M
The pOH can be calculated from this hydroxide ion concentration. Then the pH can be calculated.
pOH = -log([OH-]) = -log(0.03278 ...) = 1.48
pH = 14.00 - pOH
pH = 12.52
Example 5: 30.0 mL of 2.00 M NaOH added to 40.0 mL of 1.00 M HA
The procedure can be repeated for the addition of 20.0 mL of NaOH. This is a considerable distance past the equivalence point. Begin with a stoichiometry analysis:
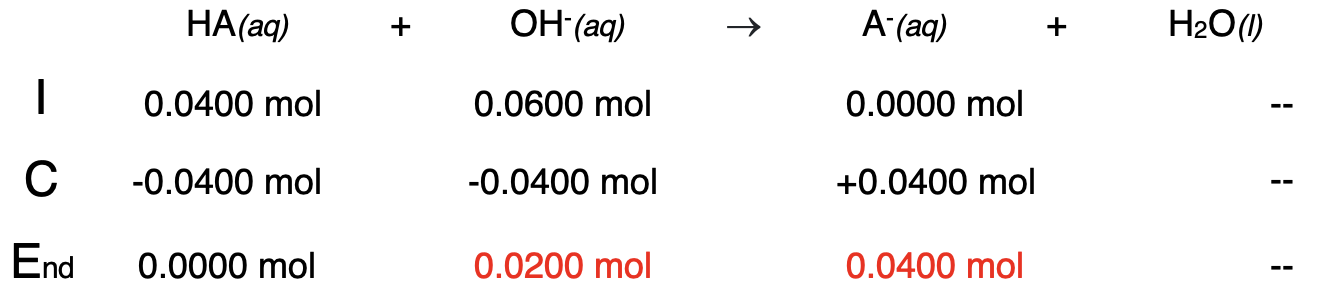
Once again, our analysis shows that there are two bases present in the solution - OH- and A-. The OH- is the stronger base and will be the determinant of the pH. The OH- is calculated and then used to determine the pOH and the pH.
[OH-] = 0.0200 mol / 0.0700 L = 0.2857 ... M
pOH = -log([OH-]) = -log(0.2857 ...) = 0.54
pH = 14.00 - pOH
pH = 13.46
Summary - After the Equivalence Point
The calculations shown in Examples 4 and 5 involved first analyzing the stoichiometry of the neutralization reaction in order to determine what species were present. After the equivalence point, it is hydroxide ions (OH-) and the anion of the weak acid that will be present. Both are bases. The hydroxide ion is a stronger base and will determine the pH of the solution. The [OH-] is calculated and then used to determine the pOH and the pH of the solution.
Results of additional calculations are shown below.
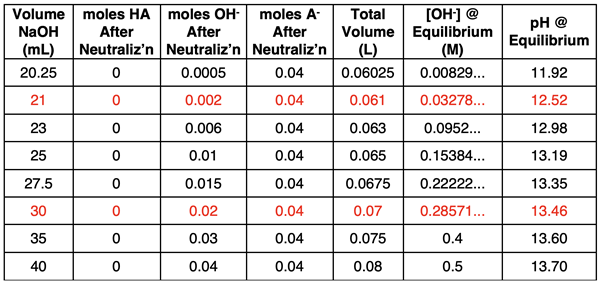
Finally, data from a spreadsheet for NaOH volumes from 0.00 mL to 35.00 mL in 0.25-mL increments are plotted and shown in the graph at the right.
It is worth a few moments to reflect on the idea that there are people who can mathematically predict an entire pH curve for the titration of a weak acid with a strong base. Those people are called Chemistry students. You are one of those people. Dataway! The ideas from Chapter 15 and Chapter 16 of this Tutorial is all that you need to prevent the pH value for any given volume of base.
Before You Leave - Practice and Reinforcement
Now that you've done the reading, take some time to strengthen your understanding and to put the ideas into practice. Here's some suggestions.
- Our Calculator Pad section is the go-to location to practice solving problems. You’ll find plenty of practice problems on our Solution Equilibria page. Check out the following problem set: Set SAB13: pH Curves for Titrations
- Download our Study Card on pH Curves for Titrations. Save it to a safe location and use it as a review tool. (Coming Soon.)