Lesson 2: Acid-Base Equilibria

Part d: Determination of the pH of Salts

Part a: Weak Acid and Weak Base Dissociation
Part b: Percent Dissociation and K_a and K_b
Part c: Dissociation of Polyprotic Acids
Part d: Determination of the pH of Salts
Part e: Common Ion Effects and Buffers
Part f: Titration Analysis

 

The Big Idea

Determining the pH of salt solutions involves understanding hydrolysis, the relationship between K_a and K_b, and the use of an ICE table to relate equilibrium concentrations to an equilibrium constant value.

 

What is Hydrolysis?

A salt is an ionic compound consisting of a cation (a positive ion) and an anion (a negative ion). When a salt dissolves in water, it dissociates into its ions. Often times, the ions of a salt can react with water, either by donating a proton to water or accepting a proton from water. Since these reactions produce hydronium (H₃O⁺) or hydroxide ions (OH^-), they affect the pH of the solution. In acid-base chemistry, these reactions of a salt with water are referred to as hydrolysis.
 
The hydrolysis of salts was discussed in great detail in Chapter 15 of our Chemistry Tutorial. On this page, we will take that discussion further by discussing how to determine the pH of a solution containing a salt that undergoes hydrolysis. We assume an understanding of hydrolysis in our discussion. Those who need to establish a sturdy background understanding of the topic should visit our page titled Predicting and Explaining the Acidity Level of Salts.
 
 
 

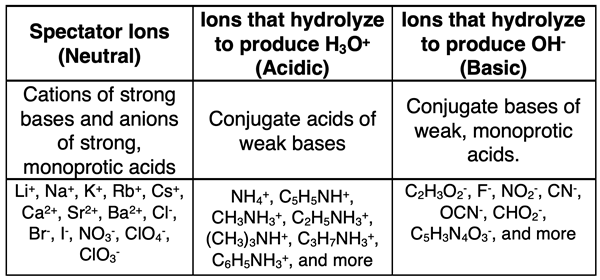
How to Predict the Ions that Hydrolyze

Some ions of salts do not hydrolyze. These include ions that are the cations of strong bases or the anions of strong, monatomic acids. Such ions behave as spectator ions in aqueous solutions.
 
Some ions of salts hydrolyze by donating a proton to water to produce H₃O⁺. These include ions that are the conjugate acids of weak bases. An example would include the ammonium ion, NH₄⁺. It is the conjugate acid of NH₃, a weak base. The ammonium ion is present in salts such as NH₄Cl and NH₄NO₃. When either of these salts dissociate, the ammonium ion separates from the anion and then undergoes hydrolysis:

NH₄⁺(aq)    +    H₂O(l)    ⇄    NH₃(aq)    +    H₃O⁺(aq) 

 
Some ions of salts hydrolyze by accepting a proton from water to produce OH^-. These include ions that are the conjugate bases of weak acids. An example would include the fluoride ion, F^-. It is the conjugate base of HF, a weak acid. The fluoride ion is present in salts such as NaF and KF. When either of these salts dissociate, the fluoride ion separates from the cation and then undergoes hydrolysis:

F^-(aq)    +    H₂O(l)    ⇄    HF(aq)    +    OH^-(aq) 

 
A summary of these ideas is shown in the table below. Further discussion and elaboration can be found on our Chapter 15 page titled Predicting and Explaining the Acidity Level of Salts.

 
 

 
 
 

Determining the K Values for Hydrolysis Reactions

Hydrolysis reactions are reversible reactions with equilibrium positions that typically lie on the reactant side. Like any acid-base equilibrium system, the determination of the pH requires a knowledge of the equilibrium constant. An ion that hydrolyzes by donating a proton to water is acting as an acid. Its hydrolysis reaction is described by a K_a value. An ion that hydrolyzes by accepting a proton from water is acting as a base. Its hydrolysis reaction is described by a K_b value.
 
The K_a and K_b values for hydrolysis reactions can be determined by identifying the conjugate of the ion that hydrolyzes. An ion such as NH₄⁺ that acts as an acid is the conjugate of the weak base NH₃. The K_a value for the hydrolysis of NH₄⁺ is determined by the equation

K_a of NH₄⁺ = 1.0 x 10^-14 / K_b of NH₃

 
An ion such as F^- that acts as a base is the conjugate of the weak acid HF. The K_b value for the hydrolysis of F^- is determined by the equation

K_b of F^- = 1.0 x 10^-14 / K_a of HF

 
The table below includes other examples of ions that hydrolyze and the logic for determining the K values for its hydrolysis reaction.

 
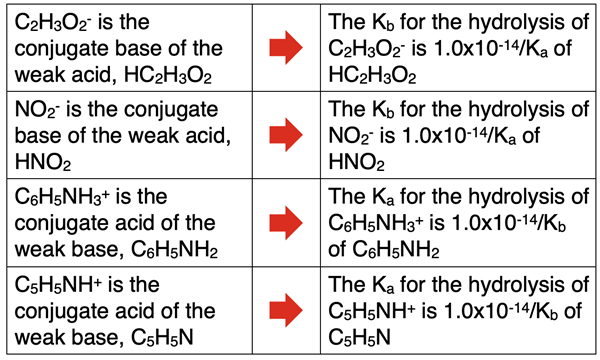
As an example calculation, let’s determine the K_b value of the acetate ion, C₂H₃O₂^-. The K_a of its conjugate acid (HC₂H₃O₂) is 1.8x10^-5. Therefore,

K_b of C₂H₃O₂^- = 1.0 x 10^-14 / 1.8 x 10^-5 = 5.6 x 10^-10

 
As a second example calculation, let’s determine the K_a value of the anilinium ion, C₆H₅NH₃⁺. The K_b of its conjugate base (C₆H₅NH₂) is 7.1x10^-10. Therefore,

K_a of C₆H₅NH₃⁺ = 1.0 x 10^-14 / 7.1x10^-10 = 1.4 x 10^-9

 
 
In all these relationships, the 1.0x10^-14 value is the ion product constant (K_w) of water. The K_w value is temperature dependent. We assume a temperature of 25°C throughout this chapter.
 
Those needing a more detailed discussion of how to determine the K value of a hydrolysis reaction can learn more on our Chapter 15 page titled K_a and K_b Values of Conjugate Acid-Base Pairs.
 
 
 
 

How to Determine the pH of a Salt Solution

The process of determining the pH of a salt solution involves the following steps:

1. If given the formula (or the name) of the salt, identify the two ions that it contains. (Need help? Visit Identifying the Ions in an Ionic Compound.)
2. Determine which of the two ions will hydrolyze. If neither hydrolyzes, then the pH is 7.0. (Need help? Visit What Ions are Acidic or Basic in Aqueous Solutions?)
3. Write the balanced chemical equation for the hydrolysis of the ion. One of the products will be either H₃O⁺ or OH^-. (Need help? Visit Hydrolysis of Salts.)
4. Calculate the K_a or K_b for the hydrolysis reaction. (Need help? See Determining K Values of Hydrolysis Reactions.)
5. Write the equilibrium constant equation that relates the K value to the equilibrium concentrations of the ions. (Need help? Visit Writing K Expressions.)
6. Set up an ICE table to determine expressions for the equilibrium concentrations. These expressions will usually include an unknown - x. Use the Five-Percent Rule if necessary.
7. Substitute the equilibrium expressions into the equilibrium constant equation from Step 5 and use algebra to solve for x.  Check to ensure that the Five-Percent Rule is a valid assumption.
8. Use the ICE table to relate the value of x to either [H₃O⁺] or [OH^-]. Use this concentration value to determine the pH. (Need help? Visit Calculting the pH from Hydronium Ion Concentration.)

 
We will demonstrate the use of this strategy in Examples 1 and 2. There are additional practice problems with complete solutions in the Check Your Understanding section.  
 
 

Example 1 - Determining the pH of a 0.50 M NH₄Cl_(aq)

Determine the pH of an aqueous solution of 0.50 M NH₄Cl. (NH₃ is a weak base with a K_b value of 1.8x10^-5.)
 
 

Solution

Step 1: NH₄Cl is a salt that contains ammonium ions (NH₄⁺) and chloride ions (Cl^-).
 
Step 2: The NH₄⁺ is the conjugate acid of a weak base (NH₃). It will hydrolyze by donating a proton to water. The Cl^- is a spectator ion; it is the anion of a strong acid (HCl).
 
Step 3: The balanced equation for the hydrolysis reaction is:  
Step 4: The K_a for this reaction is  
Step 5: The equilibrium constant equation for this hydrolysis reaction is:  
Step 6: The completed ICE table is shown below. The [NH₄⁺]_initial is equal to the concentration of the salt. The product concentrations are initially 0. A +x and a -x can be used for the change in concentration. The equilibrium concentration is always the initial concentration plus the change in concentration. We assume that 0.50 - x  ≈ 0.50. After determining x, we will check the validity of the assumption using the Five-Percent Rule.
   
Step 7: Concentration expressions from the Equilibrium row of the ICE table can be substituted into the equilibrium constant equation (step 5). (The unrounded value of K_a is used in the solution; we will round our final answer to two significant digits.) The algebraic steps for determining x are shown:
   
(The value of x is less than 5% of the 0.50 value. Thus, the assumption that 0.50 - x  ≈ 0.50 is a valid assumption.)
 
Step 8: The value of x is defined in the Equilibrium row of the ICE table as the [H₃O⁺]. This concentration value can be used to determine the pH. The work is shown here.
   
 
 
 

Example 2 - Determining the pH of a 0.50 M NaF_(aq)

Determine the pH of an aqueous solution of 0.50 M NaF. (HF is a weak acid with a K_a value of 6.6×10^-4.)
 
 

Solution

Step 1: NaF is a salt that contains sodium ions (Na⁺) and fluoride ions (F^-).
 
Step 2: The F^- is the conjugate base of a weak acid (HF). It will hydrolyze by accepting a proton from water. The Na⁺ is a spectator ion; it is the cation of a strong base (NaOH).
 
Step 3: The balanced equation for the hydrolysis reaction is:  
Step 4: The K_b for this reaction is  
Step 5: The equilibrium constant equation for this hydrolysis reaction is:  
Step 6: The completed ICE table is shown below. The [F^-]_initial is equal to the concentration of the salt. The product concentrations are initially 0. A +x and a -x can be used for the change in concentration. The equilibrium concentration is always the initial concentration plus the change in concentration. We assume that 0.50 - x  ≈ 0.50. After determining x, we will check the validity of the assumption using the Five-Percent Rule.
   
Step 7: Concentration expressions from the Equilibrium row of the ICE table can be substituted into the equilibrium constant equation (step 5). (The unrounded value of K_b is used in the solution; we will round our final answer to two significant digits.) The algebraic steps for determining x are shown:
   
(The value of x is less than 5% of the 0.50 value. Thus, the assumption that 0.50 - x  ≈ 0.50 is a valid assumption.)
 
Step 8: The value of x is defined in the Equilibrium row of the ICE table as the [OH^-]. This concentration value can be used to determine the pH. The work is shown here.
   
 

Practice Makes Perfect

As with any problem-solving skill in Chemistry, it is important to put the skill into practice. See the suggestions in the Before You Leave section for some practice and reinforcement opportunities.
 
 
 

Before You Leave - Practice and Reinforcement

Now that you've done the reading, take some time to strengthen your understanding and to put the ideas into practice. Here's some suggestions.
 

• Our Calculator Pad section is the go-to location to practice solving problems. You’ll find plenty of practice problems on our Solution Equilibria page. Check out the following two problem sets:  Set SAB10: Hydrolysis of Salts 1 || Set SAB11: Hydrolysis of Salts 2
• The Check Your Understanding section below includes questions with answers and complete solutions. It provides a great chance to self-assess your understanding.
• Download our Study Card on Determining the pH of Salts. Save it to a safe location and use it as a review tool.

 
 
 

Check Your Understanding

Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
 
1. Consider an aqueous solution of 0.420 M KNO₂. (KOH is a strong base. HNO₂ is a weak acid with a K_a value of 4.00 x 10^-4).

1. The pH of the solution will be affected by the _____ ion. 

Choices:    K⁺ ion       or       NO₂^- ion

 ​

​
 
 
 
b.   The reaction that occurs after KNO₂ dissociates is …

Choice A: K⁺_(aq) + H₂O_(l) ⇄ KOH_(aq) + H⁺_(aq)
Choice B: NO₂^-_(aq) + H₂O_(l) ⇄ HNO_2(aq) + OH^-_(aq)

​ 

​
 
 
 
c.   The equilibrium constant of the selected reaction is ______.

​  ​
 
 
 
d.   Determine the equilibrium concentration of OH^-. Use an ICE table.
 
​ ​
 
 
 
e.   Determine the pH of the solution.
 
​
 
 
 
 
 
2. Use an ICE table to calculate the pH of a 2.4 M KCN solution. The K_a of HCN is 6.20 x 10^-10.
  ​
 
 
 
3. Use an ICE table to calculate the pH of a 0.25 M KClO solution. The K_a of HClO is 3.50 x 10^-8.
  ​
 
 
 
4. Use an ICE table to calculate the pH of a 2.5 M solution of (CH₃)₂NH₂Cl. The K_b of (CH₃)₂NH is 5.40 x 10^-4.