Lesson 2: Acid-Base Equilibria

Part b: Percent Dissociation and K_a and K_b

Part a: Weak Acid and Weak Base Dissociation
Part b: Percent Dissociation and K_a and K_b
Part c: Dissociation of Polyprotic Acids
Part d: Hydrolysis of Salts
Part e: Common Ion Effects and Buffers
Part f: Titration Analysis

 

The Big Idea

Percent dissociation measures how much of a weak acid ionizes in solution, linking directly to Ka values. Understanding this relationship makes it easier to solve acid dissociation problems.

 

What is Percent Dissociation?

While a strong acid is said to undergo complete dissociation, a weak acid only partially dissociates. There is a strong reverse reaction with the equilibrium position lying on the reactant side. The undissociated acid molecules are the predominant species in solution; ion concentrations are considerably smaller. The acid dissociation constant (K_a) provides a relative measure of the extent to which the dissociation occurs.
 
A quantity referred to as the percent dissociation provides a second measure of the extent to which the acid dissociates. As the name implies, percent dissociation indicates what percentage of the original amount of acid present has dissociated into ions. The numerator and denominator of the fraction is commonly expressed in molarity units The equation is

 
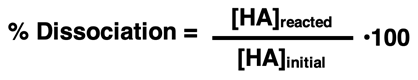
Our approach to acid dissociation problems is heavily reliant upon an ICE table (shown below). The initial concentration of acid – [HA]_initial -  is listed in the top or Initial row of the ICE table. This value is often provided in the problem statement. The amount of acid that is reacted is listed in the middle or Change row of the table. This value is sometimes calculated by substituting the concentration expressions in the bottom or Equilibrium row into the K_a equation.

 

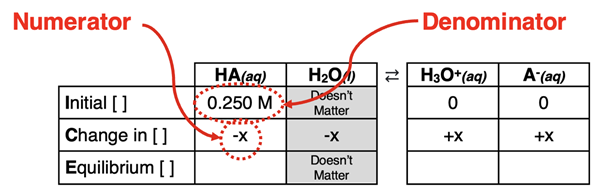
It is safe to say that no two acid dissociation problems are ever the same. But a solid understanding of the important relationships and a consistent approach will remedy a lot of the student difficulties with such problems. Let’s discuss an approach and then put it to use through several examples.

  

 
 

Problem-Solving Strategy for Percent Dissociation Problems

There are a variety of problem types in Lesson 2. While the approach to each type of problem may vary slightly, nearly every problem will share these strategic steps.

1. Write the balanced equation for the acid-base reaction.
2. Write the equilibrium constant equation for the reaction.
3. Set up and complete an ICE table that is consistent with the given information. There will typically be a blend of numerical values and unknown variables (i.e., x) in the table cells. If the percent dissociation value is given, then use it to determine x. If it is is not known, then the table will need to be used to determine x.
4. Substitute values and expressions from the equilibrium row of the ICE table into the equilibrium constant equation.
5. Use algebra to solve for the unknown quantity.

 
As we proceed through this Lesson, we will use these steps as we approach each problem.
 
 
 

Example 1 – Calculating the Percent Dissociation

Calculate the percent dissociation of a 0.20 M solution of butanoic acid (HC₄H₇O₂). Its K_a value is 1.5×10^-5.

 

Solution

Step 1: The butanoic acid will transfer a proton to water and form its conjugate base (C₄H₇O₂^-). The water accepts the proton and becomes its conjugate acid (H₃O⁺). The balanced equation is:
   
Step 2: The equilibrium constant equation is:  
Step 3: The completed ICE table is shown below. Liquids are not included in the equilibrium constant equation. As such, we do not worry about the water column of the ICE table. The Initial concentration of HC₄H₇O₂ is 0.20 M (given). The ion concentrations are initially 0 M. The reaction proceeds to the right to reach equilibrium, meaning that the reactant amounts decrease by x mol/L while the product amounts increase by x mol/L. The Equilibrium row of the table is always the Change row added to the Initial row. Presumably, x is a very small number since weak acids only partially dissociate. The result is that the 0.20 - x is approximately equal to 0.20. For instance, if x were 0.00010, then
   
This simplifies the algebra associated with the solution. We regard the assumption that 0.20 - x  » 0.20 to be valid if the value of x is less than 5% the initial concentration of the acid. That is, the assumption is valid in cases where the percent dissociation is less than 5%. This is often referred to as the 5% Rule.
   
Step 4: The value of K_a and the values and expressions in the equilibrium row of the ICE table are substituted into equilibrium constant equation from Step 2.
   
Step 5: The unknown quantities in this problem are the concentrations of the two ions - H₃O⁺ and C₄H₇O₂^-. As shown in the last row of the ICE table, these concentrations are equal to x. Algebra is performed on the equation in Step 4 to solve for x.
   
The percent dissociation can now be calculated:
   
 
 

Example 2 – Use Percent Dissociation to Determine K_a and pH

A 1.5 M solution of a weak acid has a percent dissociation of 2.8%. Determine the value of K_a and the pH of the solution.
 
 

Solution

Step 1: We will represent the weak acid by the generic formula HA. It will transfer a proton to water and form its conjugate base (A^-). The water accepts the proton and becomes its conjugate acid (H₃O⁺). The balanced equation is:
   
Step 2: The equilibrium constant equation is:
   
Step 3: The completed ICE table is shown below.
   
Since we know the percent dissociation, we can determine the value of x. The value of x must be 2.8% the value of [HA]_initial.
   
By substituting this value of x into expressions in the last row of the ICE table, we determine that ...
   
Step 4: These values of concentrations in the equilibrium row of the ICE table are substituted into equilibrium constant equation from Step 2 to determine the value of K_a.
   
Step 5: The pH can be determined using the equation from Chapter 15 of our Chemistry Tutorial: pH = -log([H₃O⁺]) where [H₃O⁺] is 0.042 M.
   
 
 

Example 3 – Use pH to Determine K_a and Percent Dissociation

A 0.80 M solution of a weak acid has a pH of 3.62. Determine the value of K_a and the percent dissociation.
 
 

Solution

Step 1: The weak acid is represented by the generic formula HA. It transfers a proton to water and form its conjugate base (A^-). The water accepts the proton and becomes its conjugate acid (H₃O⁺). The balanced equation is:
   
Step 2: The equilibrium constant equation is:
   
Step 3: The completed ICE table is shown below.
   
The pH of 3.62 is related to the hydronium ion concentration. We will use an equation from Chapter 15 of our Chemistry Tutorial to calculate the hydronium ion concentration from the pH.
   
The [H₃O⁺] is equal to the x in the ICE table and can be used to determine all the equilibrium concentrations.
   
Step 4: These equilibrium concentrations can be substituted into equilibrium constant equation from Step 2 to determine the value of K_a.
   
Step 5: The percent dissociation equation can be used to determine the percent dissociation.
   
 
 

Some Advice

Solving K_a problems may be one of the most difficult tasks in Chemistry. More than ever, a conscientious student must commit to practice. View solutions to problems and try many on your own. And try the same problem more than once ... especially if you didn’t get it right the first time. Don’t force a problem to be like previous problems. It’s a bit like putting together a puzzle. The pieces can’t be forced into a position where they don’t belong. You often have to try a puzzle piece in a position to see if it fits or turn it around and try it a different way. When it comes to solving K_a problems, there’s great benefit in participating in a cycle that follows the pattern of fail, learn, try again, and succeed.
 
 
 
 

Before You Leave - Practice and Reinforcement

Now that you've done the reading, take some time to strengthen your understanding and to put the ideas into practice. Here's some suggestions.
 

• Our Calculator Pad section is the go-to location to practice solving problems. You’ll find plenty of practice problems on our Solution Equilibria page. Check out the following problem sets:  Set SAB7: K_a, K_b, pH, and Percent Dissociation 1 || Set SAB8: K_a, K_b, pH, and Percent Dissociation 2
• The Check Your Understanding section below includes questions with answers and explanations. It provides a great chance to self-assess your understanding.
• Download our Study Card on Solving Percent Dissociation Problems. Save it to a safe location and use it as a review tool. (Coming Soon.)

 

 
 

Check Your Understanding of Percent Dissociation Problems

Use the following questions to practice the skill at solving percent dissociation problems. Tap the Check Answer buttons when ready.
 
1. Acetic acid, HC₂H₃O₂, has a K_a value of 1.8x10^-5.
a. Determine the % dissociation of a 1.0 M solution.

b. Determine the % dissociation of a 0.10 M solution.
​


c. For a fixed temperature, the K_a value is a constant. Is the % dissociation a constant or is it affected by acid concentration?
​



 
 
2. A 2.5 M solution of a weak acid undergoes 1.95% dissociation. Determine the equilibrium concentrations, the pH of the solution, and the K_a of the acid.
​



3. Determine the K_a and percent dissociation of a 1.5 M weak acid solution that has a pH of 2.88.​