Lesson 2: Acid-Base Equilibria

Part e: Common Ion Effects and Buffers

Part a: Weak Acid and Weak Base Dissociation
Part b: Percent Dissociation and K_a and K_b
Part c: Dissociation of Polyprotic Acids
Part d: Determination of the pH of Salts
Part e: Common Ion Effects and Buffers
Part f: Titration Analysis

 

The Big Idea

This page explains how the common ion effect shifts equilibrium and plays a central role in the function of buffers, allowing solutions to resist drastic pH changes. Learn to use ICE tables and the equilibrium model to analyze such systems and predict their pH.

 

  

What is a Common Ion?

Thus far in Lesson 2 we have analyzed situations in which an acid, a base, or a salt dissolves in pure water. In Lesson 2e, the situation changes. We will analyze situations in which ...

• a weak acid dissolves in a solution containing its conjugate base, and
• a weak base dissolves in a solution containing its conjugate acid.

 
As an example of the first situation, consider the dissolving of HF (a weak acid) in an aqueous solution of NaF (a soluble salt). The acid, as is its usual case, will donate a proton to water to form hydronium ions (H₃O⁺) and its conjugate base (F^-).
   
This situation is unique in that the conjugate base is already present in the solution. As this situation is analyzed using an ICE table, the initial concentration of the conjugate base is not 0 M. Suppose a 0.50 M solution of HF is prepared with a 0.50 M solution of NaF. The NaF completely dissociates, leading to an initial concentration of F^- ions of 0.50 M.
   
In this situation, the acid (HF) and the salt (NaF) have an ion in common - that is, a “common ion.” The common ion is F^-. It is present in both the acid and the soluble salt and must be included in the ICE table and subsequent analysis.
 
Of course, there are numerous situations which involve a weak acid and a salt containing a common ion. Here are a few:
 

• The weak acid HC₂H₃O₂ dissolving in a salt solution of NaC₂H₃O₂.
• The weak acid HCN dissolving in a salt solution of KCN.
• The weak acid HNO₂ dissolving in a salt solution of NaNO₂.

 
In each of these situations, there is an ion that both the weak acid and the salt have in common. The common ion is the conjugate base of the weak acid.
   
 

A Weak Acid in Pure Water vs. a Weak Acid in a Salt Solution

Let’s contrast the pH analysis of these two situations:  
The Situation 1 analysis (or ones like it) has been conducted numerous times in Lesson 2 (see Weak Acid and Weak Base Dissociation). A quick run through is shown below.
   
The Situation 2 analysis will look very similar, with the exception that there is a common ion, causing the initial [F^-] to not be 0 M. Note that the [F^-] in the Initial row is 0.50 M, identical to the concentration of the salt (NaF). The presence of this common ion will have a significant effect on the pH of the equilibrium system. The solution is shown below:
   
Without the common ion, the pH of the 0.50 M HF solution is 1.74. But with the common ion, the pH of the 0.50 M HF solution is 3.18.  The presence of the common ion reduces the tendency of the acid to dissociate. With less acid dissociating in the common ion solution, the hydronium ion concentration is smaller and the pH value is larger. This is known as the common ion effect.  
 

Example 1 - pH of a HC₂H₃O₂ | NaC₂H₃O₂ System

Repeat a similar analysis to determine the pH of a solution consisting of 0.50 M HC₂H₃O₂ with 0.25 M NaC₂H₃O₂. The K_a of HC₂H₃O₂ is 1.8 x 10^-5.
 
 

Solution

This problem features a weak acid (HC₂H₃O₂) in a solution containing its conjugate base (C₂H₃O₂^-). The acid will do what acids do - donate a proton to water. Begin by writing the dissociation equation for the acid.
   
This is an equilibrium system and equilibrium concentrations can be related to the K_a value. The next step is to write the equilibrium constant equation.
   
Now an ICE table is set up to show the progression from initial conditions to the equilibrium conditions. The initial concentration of the common ion must be included in the Initial row of the table. The Five-Percent Rule can be used to simplify the mathematics (see Equilibrium row). The assumption is that x is so small that
   
After solving for x, we will check to ensure that its value is less than 5% of 0.25.
   
The concentration expressions from the equilibrium row of the table are substituted into the equilibrium constant equation. Then algebra is used to solve for x.  
The value of x is less than 5% of 0.25. Our assumptions to neglect the effect of x on [HC₂H₃O₂] and on [C₂H₃O₂^-] are valid.
 
Based on the Equilibrium row of the table, the value of x is equal to the [H₃O⁺]. It can be used to determine the pH.
   
 
 

LeChatelier’s Principle and the Common Ion Effect

We discussed LeChatelier’s Principle in Chapter 14 of our Chemistry Tutorial. The principle suggest that equilibrium systems respond to disturbances or stress by attempting to counteract the stress. A common ion situation is different than a straightforward acid dissociation situation in that there is an addition of a product ion. The system responds to the addition of products by attempting to react this product away. This product ion causes the equilibrium position to shift towards reactants. Less product is produced compared to the situation of a weak acid in pure water. This means that the hydronium ion concentration (the other product) will be smaller at equilibrium when the common ion is present. This is the common ion effect.
   
 
 

How Does the Concentration of the Common ion Effect the pH?

Let’s assume the generic acid HA is present in solution with a salt containing the common ion, A^-. Let’s develop an equation that relates the pH of the solution to the K_a of the acid and the concentrations of HA and A^-. The ICE table for this situation is shown.
   
The equilibrium constant equation is
   
Substituting the expressions from the Equilibrium row of the ICE table yields:
     
The pH can be determined from the [H₃O⁺].
   
This equation is sometimes referred to as the Henderson-Hasselbalch equation. It allows us to calculate the pH of a solution containing a weak acid (HA) and a soluble salt containing its conjugate base (A^-).
 
Let’s use the equation to determine the pH of an HC₂H₃O₂ | NaC₂H₃O₂ system with an acid concentration of 1.00 M and a conjugate base concentration that varies from 0.00 M to 2.00 M. The K_a of HC₂H₃O₂ is 1.8×10^-5. The table shows the results of the calculations. The use of the Henderson-Hasselbalch equation to calculate the pH of the solution is shown in the last column of the table.
   
As can be seen in the table, increases in the concentration of the common ion leads to increases in the pH. The greater the concentration of the common ion, the less that the acid dissociates and the less acidic (higher pH) the solution is. Put another way, the common ion effect becomes more pronounced as the concentration of the common ion is increased.
   
 

A Weak Base with a Salt Containing its Conjugate Acid

Now let’s consider a weak base (NH₃) dissolving in a solution with a soluble salt containing its conjugate acid (NH₄Cl). Let’s analyze a situation in which both the weak base and the salt have a concentration of 0.50 M. The K_b of NH₃ is 1.8x10^-5. We wish to determine the pH of the solution.
 
The NH₃ will do what bases always do - accept a proton from water. The equation for the base dissociation reaction is
   
The equilibrium constant equation is for this reversible system is
   
An ICE table can be constructed to facilitate the analysis. The concentration of the ammonium ion (NH₄⁺) equals the concentration of the salt that contains it.
   
Concentration expressions in the Equilibrium row of the table can be substituted into the equilibrium constant equation. Algebra can be used to solve for x.
     
The value of x represents the hydroxide ion (OH^-) concentration. The pOH and pH can be calculated from this value.
  In contrast to this common ion situation, the pH of a 0.50 M solution of NH₃ in otherwise pure water would be 11.48. For solutions of a weak base and a salt containing its conjugate acid, the common ion effect decreases the amount of dissociation, the relative alkalinity of the solution, and the pH of the solution.
 
 
 

Example 2 - pH of a Weak Base and a Salt Containing its Conjugate Acid

An aqueous solution of ethylamine (C₂H₅NH₂) and a salt containing its conjugate acid (C₂H₅NH₃Cl) is prepared. The initial concentrations are:  
The reaction is:
   
The K_b of C₂H₅NH₂ is 5.60 x 10^-4. Use an ICE table to determine the pH of the solution.
 
 

Solution

The C₂H₅NH₂ acts as a base, accepting a proton from water. The equation for its dissociation reaction was provided
   
The equilibrium constant equation is for this reversible system is
   
An ICE table is used to facilitate the analysis. The initial concentration of the ethylamine (C₂H₅NH₂) and the ethylammonium ion (C₂H₅NH₃⁺) were given.
   
Concentration expressions from the Equilibrium row of the table can be substituted into the equilibrium constant equation. Algebra can be used to solve for x.
     
The value of x represents the hydroxide ion (OH^-) concentration. The pOH and pH can be calculated from this value.  
 
 

Procedure for Analyzing a Common Ion Problem to Determine the pH

Each of our examples of determining the pH of a common ion situation have followed the following steps:

1. Identify the weak acid and its conjugate base (or the weak base and its conjugate acid).
2. Write the dissociation equation.
3. Write the equilibrium constant equation relating the K_a (or K_b) value to the equilibrium concentrations of aqueous-state substances.
4. Complete an ICE table to show the progression of the system from initial concentrations to equilibrium concentrations.
5. Substitute expressions for equilibrium concentrations into the equilibrium constant equation from step 3.
6. Use algebra to determine the value of x.
7. Refer to the Equilibrium row of the ICE table to relate x to either [H₃O⁺] or [OH^-]. Then calculate the pH.

 
 
 

What is a Buffer?

A solution that consists of a weak acid and its conjugate base (or a weak base and its conjugate acid) is described as an acid-base buffer. More generally, the word buffer is used in English to describe a person or thing that provides protection or acts as a barrier against harm, shock, or other negative impacts. In the automobile world, the bumper on a car acts as a buffer, protecting the occupants from harm and shock in front-end collisions. In the computing world, a buffer is a temporary storage unit that stores video data to reduce the impact caused by suddenly slow download speeds. And in chemistry, a buffer protects a chemical system from abrupt pH changes that result from the addition of acids and bases. An acid-base buffer is a solution that resists changes in pH when small amounts of acid or base are added to it. Just as the bumper on a car acts as a shock absorber, an acid-base buffer acts as a pH shock absorber.
 
 
 

How do Buffers Work?

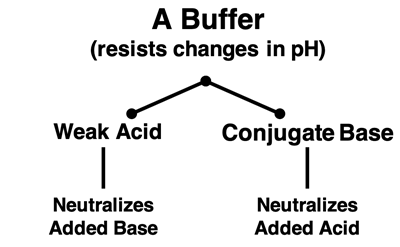
A buffer solution consists of a weak acid and its conjugate base OR of a weak base and its conjugate acid. This means that a buffer solution contains both an acid and a base. This acid and base act as a team to help the solution resist changes when an acid or a base is added to the solution. If an acid is added to a buffer solution, the base reacts with the acid to neutralize it. And if base is added to the buffer solution, the acid reacts with it to neutralize it. This acid-base team reduces the impact of any added acid or base and protects the solution from the shock caused by a pH change.
 
Think of a sponge as being analogous to an acid-base buffer. A sponge provides protection against water spills. If water is poured onto a sponge, the sponge absorbs the water. By soaking up the water, the sponge prevents a puddle. In the same manner, an acid-base buffer soaks up any added acid or base that is poured into the solution and prevents a drastic pH change.
   
Fluids within the body (such as blood) are equipped with buffer systems that help to stabilize the pH. The most common buffer system, found in our blood, includes carbonic acid (H₂CO₃) and the bicarbonate ion (HCO₃^-). The bicarbonate ion reacts with excess hydrogen ions to prevent sudden decreases in the pH. And the carbonic acid releases hydrogen ions to neutralize bases and prevent sudden increases in the pH of the blood. Maintaining a stable blood pH between 7.35 and 7.45 is critical for human health. Deviations outside of this narrow range can lead to serious health effects. Without this critical buffer system, we would not survive. For certain, that’s Chemistry for Better Living!
 
 
 

Before You Leave - Practice and Reinforcement

Now that you've done the reading, take some time to strengthen your understanding and to put the ideas into practice. Here's some suggestions.
 

• Our Calculator Pad section is the go-to location to practice solving problems. You’ll find plenty of practice problems on our Solution Equilibria page. Check out the following problem set:  Set SAB12: Common Ion Problems
• The Check Your Understanding section below includes questions with answers and explanations. It provides a great chance to self-assess your understanding.
• Download our Study Card on Acids, Bases, and the Common Ion Effect. Save it to a safe location and use it as a review tool.

 
 
 

Check Your Understanding of the Common Ion Effect

Use the following questions to assess your understanding of common ion situations, the common ion effect, buffers, and the mathematics of the common ion effect. Tap the Check Answer buttons when ready.
 
1. Which of the following sets of two substances meet the criterion of being a weak acid with a conjugate base? Select all that apply.
a. HC₄H₇O₂   and   NaC₄H₇O₂
b. H₂SO₃   and   KHSO₃
c. HC₃H₃O₂   and   C₃H₃O₂Cl
d. HOCN   and   CN
 

 
2. Which of the following sets of two substances meet the criterion of being a weak base with a conjugate acid? Select all that apply.
a. NH₃   and   NaNH₂
b. C₆H₅NH₂   and   C₆H₅NH₃Cl
c. C₉H₇N   and   C₉H₇NCl
d. NH₃   and   NH₄Na
 
​


 
3. Write the formula of a sodium salt that contains the conjugate base of phosphoric acid (H₃PO₄).
 
​


 
4. A solution contains 0.50 M HNO₂ (K_a = 7.2 x 10^-4) with 0.25 M NaNO₂.
a. Write a dissociation equation for the reaction.
 
​



b. Write the equilibrium constant equation for this equilibrium system.
 
​



c. Complete an ICE table for this situation
 
​



d. Determine the hydronium ion concentration at equilibrium.
 
​



e. Calculate the pH of the solution.
 
​


 
5. Calculate the pH of a solution containing 1.50 M chlorous acid (HClO₂) with 1.25 M sodium chlorite (NaClO₂). The K_a of chlorous acid is 1.1×10^-2.
 
​


 


6. A buffer system consists of benzoic acid (HC₇H₅O₂) and sodium benzoate.
a. Identify the formula of sodium benzoate.
 


b. Describe how the system responds to stabilize the pH when NaOH is added to it.

 


c. Describe how the system responds to stabilize the pH when HCl is added to it.
 
​