Lesson 3: Acid and Base Dissociation

Part b: Dissociation Constants

Part a: Strong vs. Weak Acids and Bases
Part b: Dissociation Constants

 

The Big Idea

Dissociation constants (K_a and K_b) are equilibrium constants that measure the strength of acids and bases. This lesson explores how K_a and K_b values relate to acid-base strength, hydronium ion concentration, and pH, using diagrams, tables, and calculations.

 

What is a Dissociation Constant?

Strong and weak acids were introduced in Lesson 3a (Strong and Weak Acids and Bases). Strong acids are acids that completely dissociate into ions when dissolved in water. For every 1 mole of a strong acid dissolved in water, 1 mole of H₃O⁺ ions will be produced. Weak acids only partially dissociate. If 1 mole of a weak acid is dissolved in water, only a small portion of that weak acid will dissociate and produce H₃O⁺ ions. The exact portion that does dissociate is determined by the dissociation constant for that particular acid.
 
We represent the dissociation of a weak acid with a generic formula of HA by a reversible reaction arrow:

HA(aq)  +  H₂O(l)    ⇄    H₃O⁺(aq)   +  A^-(aq) 

The weak acid is part of a reversible system with a forward and a reverse reaction. For weak acids, the reverse reaction is the more dominant reaction and the equilibrium position lies on the reactant side. That is, the reactant concentrations are relatively large and the product concentrations are relatively small.
 
Every reversible system is described by an equilibrium constant K. For weak acid dissociation reactions, we refer to this K value as the acid dissociation constant and represent it by the symbol K_a. Applying the Law of Chemical Equilibrium discussed in Chapter 14 of our Chemistry Tutorial, we can relate the K_a value to equilibrium concentrations of the acid and its ions:

 

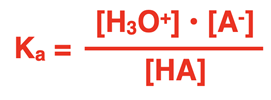
Like any K expression, the acid dissociation constant equation is always written with the concentrations of products in the numerator and the concentration of reactants in the denominator. The K_a expressions for the dissociation of hydrofluoric acid (HF) and acetic acid (HC₂H₃O₂) are shown below.

 

 

K_a and Acid Strength

For any reversible system, the equilibrium constant indicates the extent to which the reaction occurs in the forward direction. The K value is the ratio of product concentrations to reactant concentrations at equilibrium. So for a reaction that proceeds strongly in the forward direction, the product concentrations are large, the reactant concentrations are small, and the K value is much greater than 1. For a reaction that does not proceed strongly in the forward direction, the product concentrations are small, the reactant concentrations are large, and the K value is much less than 1. This is the case for weak acids.

 
For weak acid dissociation, the value of K_a indicates the extent to which dissociation occurs. Every weak acid has its own unique K_a value. The K_a values are less than 1, consistent with partial dissociation. The larger that the K_a value is, the more that the weak acid dissociates. The K_a value of nitrous acid (HNO₂) is 5.6x10^-4. The K_a value of hydrocyanic acid (HCN) is 6.2x10^-10. The considerably larger K_a value of HNO₂ means that it dissociates to a greater extent than HCN. While HNO₂ is a weak acid, it is a stronger weak acid than HNO₂. At equilibrium, the concentration of the ions will be greater in an HNO₂ solution compared to an HCN solution

 
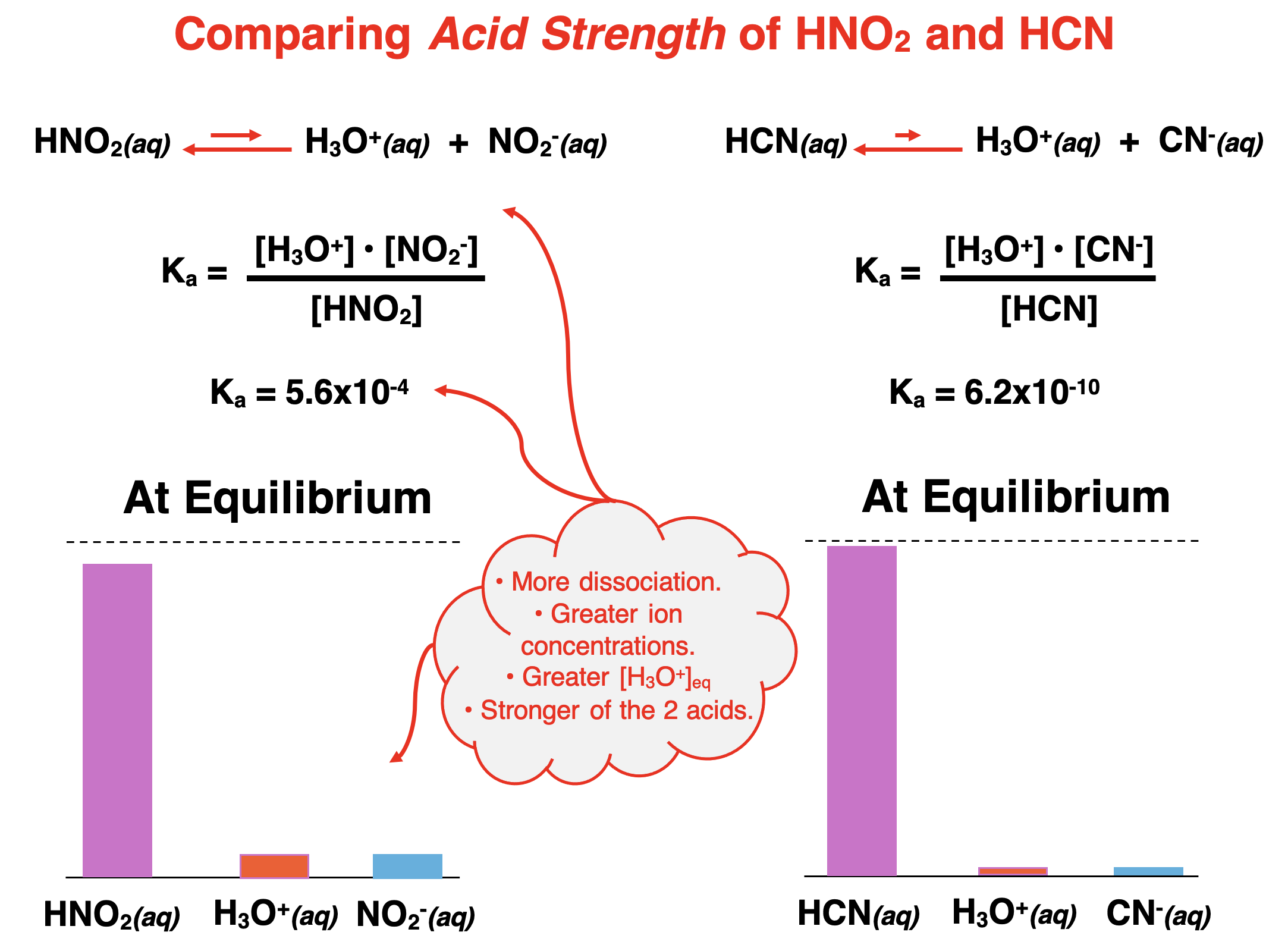
The general rule is that the larger the K_a value is for a weak acid, the more that the acid dissociates into ions, and the stronger that the acid is.
 

 
 
 

Typical Weak Acids and Their K_a Values

The table below displays K_a values for the more commonly encountered weak acids. The table is organized by K_a value. Acids with the higher K_a values are located at the top of the table. Thus, the weak acids are ordered by acid strength.
 

Name of Acid	Formula	Ka Value (@25°C)
Chlorous acid	HClO2	1.1 × 10–2	Strongest
Nitrous acid	HNO2	7.2 × 10–4
Hydrofluoric acid	HF	6.6 × 10–4
Formic acid	HCO2H	1.78 × 10−4
Acetic acid	HC2H3O2	1.8 × 10–5
Propionic acid	HC3H5O2	1.3 × 10–5
Hypochlorous acid	HClO	2.9 x 10-8
Hydrocyanic acid	HCN	6.2 x 10-10	Weakest

   
Additional examples of weak acids and their K_a values can be found in the Reference section of our Chemistry Tutorial - Dissociation Constants.
 
 
 

What are Polyprotic Acids?

The acids in the table above are called monoprotic acids. They each contain one ionizable H⁺ ion. Some acids are polyprotic acids. They may contain two or three ionizable H⁺ ions. Carbonic acid, H₂CO₃, is an example of a diprotic acid that partially dissociates. It has two ionizable H⁺ ions. The ions are removed in a stepwise fashion as shown.
   
A diprotic acid typically has two K_a values, one for each dissociation step. They are distinguished from each other as K_a1 and K_a2.
 
Phosphoric acid, H₃PO₄, is a common triprotic acid. It has three ionizable H⁺ ions that are removed in three dissociation steps as shown.
   
The most common polyprotic acid is probably sulfuric acid, H₂SO₄. Sulfuric acid is unique among polyprotic acids because it is considered a strong acid. The first H⁺ ion ionizes completely, and the conjugate base, the HSO₄^- ion, is formed. The second H⁺ ion is removed by the partial dissociation of the HSO₄^- ion. The entire process is represented as  
The table below lists several polyprotic acids and the K_a values for their dissociation steps.
 

Name of Acid	Formula	Ka1	Ka2	Ka3
Ascorbic acid	H2C6H6O6	7.9 x 10-5	1.6 x 10-12	--
Boric acid	H3BO4	5.8 x 10-10	1.8 x 10-13	1.6 x 10-14
Carbonic acid	H2CO3	4.4 x 10-7	4.7 x 10-11	--
Citric acid	H3C6H5O7	7.4x 10-4	1.7 x 10-5	4.1 x 10-7
Oxalic acid	H2C2O4	5.4 x 10-2	6.5 x 10-5	--
Phosphoric acid	H3PO4	7.1 x 10-3	6.3 x 10-8	4.2 x 10-13
Sulfuric acid	H2SO4	--	1.2 x 10-2	--
Sulfurous acid	H2SO3	1.3 x 10-2	6.3 x 10-8	--

 
Additional examples of polyprotic acids and their K_a values can be found in the Reference section of our Chemistry Tutorial - Dissociation Constants.
   
 

Calculations of K_a of a Weak Acid from pH

The K_a of a weak acid can be determined by measuring the pH value of a known concentration of the acid. The pH that results from the weak acid’s dissociation allows one to determine the hydronium ion concentration - [H₃O⁺]. This concentration is equal to the anion concentration. The K_a expression can be used to calculate the K_a for the weak acid. The following step-by-step procedure will be helpful.
   
NOTE: We will discuss weak acid dissociation problems in greater detail in Chapter 16 of our Chemistry Tutorial. We will provide a more detailed background to the above procedure in that chapter and also discuss numerous variations of weak acid and base dissociation problems.
 
 
 

Example 1 - Calculating K_a from pH

A 2.5 M aqueous solution of a weak acid is measured to have a pH of 3.8. Determine the K_a of the acid.
   
 
 

Example 2 - Calculating K_a from pH

A 2.5 M aqueous solution of a weak acid is measured to have a pH of 5.8. Determine the K_a of the acid.
   
 
 

Effect of K_a on the pH of Solution

Analysis of the two calculation results from Examples 1 and 2 reveals an important pattern. The two examples involved two different acids (different K_a values) having the same initial concentration. Their pH was different because of the differences in their K_a values. Here’s a summary of the results.
   
As can be seen from the data, the acid with the larger K_a value (Example 1) dissociated to form a solution with a higher hydronium ion concentration. The resulting pH was thus a lower pH value. The stronger the acid is, the more it dissociates to form H₃O⁺, and the lower that the pH of the solution will be.
   
 
 

Do Strong Acids Have K_a Values?

Yes, they do. And the K_a values of strong acids are always much greater than 1.0. This indicates that the reaction favors the production of products. The molar concentration of undissociated HA molecules is significantly less than the concentration of dissociated ions. For our purposes, we simply consider strong acid dissociation reactions as proceeding to completion . This is why we represent the dissociation of a strong acid by a forward reaction arrow (as opposed to the reversible reaction arrow, ⇄).
   
For strong acids, we would approximate the concentration of H₃O⁺ in solution to be equal to the concentration of the acid before it dissociated.
 
Dissociation constants for a variety of strong acids are shown in the table below.
 

Name of Acid	Formula	Ka Value
Perchloric acid	HClO4	Very Large
Hydroiodic acid	HI	3.2 × 109
Hydrobromic acid	HBr	3.2 × 109
Hydrochloric acid	HCl	1.3 × 106
Sulfuric acid	H2SO4	1.0 × 103
Chloric acid	HClO3	5.0 x 102
Nitric acid	HNO3	2.4 × 101

 
 
 

Base Dissociation and K_b Values

Like a weak acid, a weak base partially dissociates in aqueous solutions to produce its conjugate acid and hydroxide ions (OH^-). A base with the generic formula B will undergo the following dissociation reaction:
   
The extent to which this reaction occurs is reflected by the K_b value of the base. K_b is referred to as the base dissociation constant. Every base has its own unique K_b value. A large K_b value (much greater than 1) indicates that the dissociation is complete and the conjugate acid and hydroxide ions are the predominant species in the solution. For weak bases, the K_b values are less than 1.0, indicating partial dissociation.
 
Ammonia, NH₃, has a K_b value of 1.8x10^-5. As was the case for acids, the dissociation constant indicates the ratio of product concentrations to reactant concentrations. The chemical equation for the dissociation of NH₃ in water and the K_b expression are:
   
As a second example, methyl amine, CH₃NH₂, is a weak base with a K_b value of 4.4x10^-4. The chemical equation for the dissociation of CH₃NH₂ in water and the K_b expression are:
   
(Need to review? Check out our pages on Base Dissociation Equations and Writing K Expressions as needed.)
 
 
 

Common Weak Bases and Their K_b Values

The table below displays K_b values for the more commonly encountered weak bases. The table is organized by K_b value with bases having the higher K_b values being located at the top of the table. Thus, the weak base are ordered by base strength.
 

Name of Base	Formula	Kb Value (@25°C)
Piperidine	C5H10NH	1.3× 10–3	Strongest
Trimethyl amine	(CH3)3N	1.0 × 10–3
Ethyl amine	C2H5NH2	5.6 × 10–4
Methyl amine	CH3NH2	4.4 × 10–4
Ammonia	NH3	1.8 × 10–5
Hydrazine	NH2NH2	1.7 × 10–6
Pyridine	C5H5N	1.8 × 10–9
Aniline	C6H5NH2	4.3 × 10–10	Weakest

 
Additional examples of weak bases and their K_b values can be found in the Reference section of our Chemistry Tutorial - Dissociation Constants.
 
 

 
 

Before You Leave - Practice and Reinforcement

Now that you've done the reading. Take some time to strengthen your understanding and to put the ideas into practice. Here's some suggestions.
 

• The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.
• Download our Study Card on Dissociation Constants. Save it to a safe location and use it as a review tool. (Coming Soon.)
• Check out our Reference section page with concepts related to K_a and K_b values for strong and weak acids, weak bases, and polyprotic acids. When you need some data, you’ll likely find it in our Reference section.

 
 
 

Check Your Understanding of Dissociation Constants

Use the following questions to assess your understanding of K_a and K_b values. Tap the Check Answer buttons when ready.
 
1. Complete the following paragraph:
 
A strong acid _______________ (partially, completely) dissociates while a weak acid _______________ (partially, completely) dissociates. The dissociation of the _________ (strong, weak) acid is best modeled as a reversible system with a dominant _________________ (forward, reverse) reaction. The dissociation of a ____________ (strong, weak) acid is considered to proceed to completion. A solution of a weak acid will consist primarily of ___________________ (undissociated acid molecules, dissociated ions) whereas a solution of a strong acid will consist primarily of ___________________ (undissociated acid molecules, dissociated ions).  

 
 
2. The acid dissociation constant for a weak acid is ____________.

1. relatively large, much greater than 1
2. relatively small, much less than 1
3. .. come on now! This is Chemistry, not fortune telling. Do you expect things to be that predictable.

​
 
 
For Questions #3-6:  Formic acid (HCO₂H) has a K_a value of 1.8 x 10^-4 and hypochlorous acid (HClO) has a K_a value of 2.9x10^-8.
 
3. Which acid has the greatest concentration of undissolved acid at equilibrium?

1. formic acid (HCO₂H)
2. hypochlorous acid (HClO)

​
 
 
4. Which acid has the greatest concentration of hydronium ions at equilibrium?

1. formic acid (HCO₂H)
2. hypochlorous acid (HClO)

​
 
 
5. Which acid has the greatest pH value at equilibrium?

1. formic acid (HCO₂H)
2. hypochlorous acid (HClO)

​
 
 
6. Which is the stronger of the two acids?

1. formic acid (HCO₂H)
2. hypochlorous acid (HClO)

​
 
 
7. Acid A and B are both weak acids. Acid A has the larger K_a value. Which of the following statements are true of acid A? (Assume their concentrations are equal.) Select all that apply.

1. Acid A is the stronger acid.
2. Acid A has a higher pH value.
3. Acid A dissociates into ions more than acid B.
4. Acid A is more concentrated with H₃O⁺ than acid B.

​
 
 
For Questions #8-10:  Pyridine (C₅H₅N) has a K_b value of 1.8 x 10^-9 and ammonia (NH₃) has a K_b value of 1.8 x 10^-5.
 
8. Which base is the stronger base?

1. pyridine (C₅H₅N)
2. ammonia (NH₃)

​
 
 
9. Which base has the greater tendency to dissociate into ions?

1. pyridine (C₅H₅N)
2. ammonia (NH₃)

​
 
 
10. Which base has the greater pH value at equilibrium?

1. pyridine (C₅H₅N)
2. ammonia (NH₃)

​