Lesson 2: Equilibrium

Part b: Equilibrium Constant Expressions

Part a: The Equilibrium State
Part b: Equilibrium Constant Expressions
Part c: Calculations of K and Concentration
Part d: Predicting the Direction of Reaction
Part e: Analyzing Equilibrium Systems

 

The Big Idea

Equilibrium constant expressions (Kc or Kp) quantify the ratio of product to reactant concentrations (or pressures) at equilibrium, following the balanced chemical equation and the law of chemical equilibrium.

 

There are Many Equilibrium Concentrations, but One Ratio

The NO₂-N₂O₄ equilibrium system was thoroughly discussed in Lesson 2a.

2 NO₂(g)   ⇄   N₂O₄(g)

It was emphasized that reversible systems always achieve the equilibrium state regardless of the starting position. Whether the system starts with all NO₂ or all N₂O₄ or a mixture of both in any proportion, it will always progress towards and attain equilibrium. The table below depicts five trials with different starting positions and establishing different equilibrium positions.

 
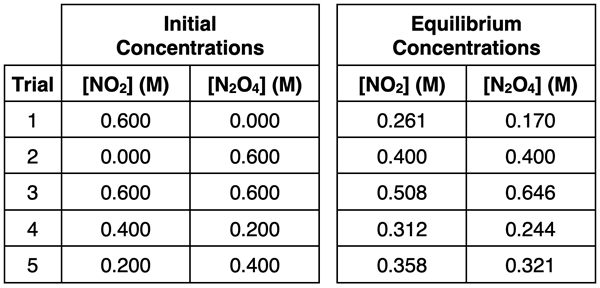
A few questions arise regarding the mathematical sense of these numbers.

• Is there any mathematical relationship that fits the equilibrium concentration data for all five trials?
• Is there any big principle that would allow one to predict the concentrations at equilibrium from the original concentrations?

 
Amazingly, the answers to both questions is yes. The focus of Lesson 2b is on the first question. We’ll begin by looking at the five equilibrium positions (sets of equilibrium concentrations). Suppose we add a column to the table in which we calculate the ratio of [N₂O₄] / [NO₂]². The calculated values are shown at the right. Observe that the values are 2.50 in every trial. This is surely more than a coincidence. 

(Note the actual value of 2.50 is unique to this reaction and is dependent upon the temperature at which the trials were performed.)
 

 
 

The Law of Chemical Equilibrium

In 1864, Norwegian chemists Cato Guldberg and Peter Wage proposed the Law of Mass Action to explain the relationship between equilibrium concentrations. The law has undergone a few revisions over time and is now more commonly referred to as the Law of Chemical Equilibrium. Suppose we consider a generic reaction with reactants A and B and products C and D. The balanced equation is written below with coefficients a, b, c, and d.
   
The Law of Chemical Equilibrium states that at any given temperature, a reversible reaction system is at equilibrium if the ratio of product to reactant concentrations, each raised to a power equal to its coefficient, is constant. In equation form, the ratio is a constant value. Provided the temperature is not changed, any set of initial concentrations will lead to a set of equilibrium concentrations that satisfy this principle.
 
The constant referred to above is known as the equilibrium constant and is represented by the symbol K (or K_c where the subscript c represents concentration). The values of K can be determined experimentally by performing a trial and measuring equilibrium concentrations. Measured concentrations are substituted into the equation and the value of K is calculated. (K values can also be determined from Thermodynamic data … to be discussed later in Chapter 17 of this Chemistry Tutorial.)
   
 

Writing K Expressions

The equilibrium constant (a numerical value) is equal to the equilibrium constant expression (a ratio of concentrations and exponents). A student of chemistry will need to develop some skill at writing the equilibrium constant expression for any given reaction. Here are attributes of the expression to be aware of:
 

• List product concentrations in the numerator and reactant concentrations in the denominator.
• Raise each concentration to a power equal to the coefficient in the balanced chemical equation.
• If there is more than one reactant (or product), then multiply their concentrations.
• Only gaseous and aqueous-state reactants and products are included in the expressions. Pure solids and liquids are omitted.

 
Use the examples below to gain some expertise at writing equilibrium constant expressions. Additional practice ideas are suggested in the Before You Leave section near the end of Lesson 2b.
   
 

Example 1 - Writing K Expressions

Write the equilibrium constant equation for the following reversible system:
 
 
 

Example 2 - Writing K Expressions

Write the equilibrium constant equation for the following reversible system:
 
 
 

Example 3 - Writing K Expressions

Write the equilibrium constant equation for the following reversible system:
 

 
 

Example 4 - Writing K Expressions

Write the equilibrium constant equation for the following reversible system:
   

 
 

Example 5 - Writing K Expressions

Write the equilibrium constant equation for the following reversible system:
   

 

 
 

The Units on K

The equilibrium constant does have units. The actual units vary from equation to equation. The units depend on the coefficients of all gaseous and aqueous state substances in the balanced chemical equation. Those coefficients can be summed for the reactants and then summed for the products. Be sure to include only gases and aqueous state substances. And be sure to include the coefficients of 1, even if they are not written. Raise mol/L or M to a power equal to the result of the product sum minus the reactant sum of these coefficients.
 
 
 

K, K_c, and K_p

The equilibrium constant for reactions that involve all gaseous-state substances (homogeneous gas phase systems) is often calculated based on partial pressures instead of concentrations. This is done because partial pressures are often easier to measure than concentrations for gaseous systems. Such an equilibrium constant is referred to as a pressure equilibrium constant and represented by the symbol K_p (the subscript p stands for pressure).
 
The rules for writing pressure equilibrium constant expressions are identical to the rules we have already used … except partial pressure symbols are used. For the generic reaction
   
the pressure equilibrium constant equation is
   
where P_A, P_B, P_C, and P_D are the partial pressures of the four gases at equilibrium.
 
A numerical value for K_p can be calculated from the K_c value for the same reaction. The equation is
   
where R = universal gas law constant (0.08206 L•atm/mol/K), T = Kelvin temperature, and ∆n equals the change in the number of moles of gas in the balanced chemical equation. The ∆n value can be determined using the coefficient in the balanced chemical equation. Subtract the sum the coefficients for all gaseous reactants from the sum the coefficients for all gaseous products. For the reaction:   
   
the ∆n is -1, meaning the number of gaseous state molecules decreased by 1. And for the reaction:  
   
the ∆n is +1, meaning the number of gaseous state molecules increased by 1.
   
 

Example 6 - Writing K_p Expressions

Write the pressure equilibrium constant equation for the following reversible system:
   
 

 

Example 7 - Writing K_p Expressions

Write the pressure equilibrium constant equation for the following reversible system:
   
 

 
 

Manipulated Reactions Require Manipulated Equilibrium Constants

Equilibrium constant values are unique to a balanced chemical equation for a reaction at a given temperature. Students will likely encounter situations in which they know the equilibrium constant for a chemical equation and will need to determine its value for a modified form of the balanced chemical equation. As an example, the K_c value for the reaction
   
at 600°C is approximately 4.2 L/mol. This means the following is true at 600°C:
   
If the chemical reaction is reversed from a synthesis to a decomposition reaction, then the equilibrium constant expression will be inverted. That is, the numerator becomes the denominator (and vice versa). To maintain an equality, the K_c value for the decomposition reaction would be the reciprocal of the synthesis reaction. In other words, for the reaction
   
at 600°C, the K_c value is approximately 1/(4.2 L/mol) or approximately 0.24 mol/L. Again, this means the following is true for the decomposition reaction at 600°C.
   
Another equation modification that can occur is that the coefficients in the balanced chemical equation might all change by a particular factor. For instance, the synthesis of SO₃ might be written such that only 1 mol of SO₃ is produced:
   
While fractional coefficients are not conventional, they do serve a purpose when one wishes to write a chemical equation for the production of 1 mole of a product that normally has a coefficient of 2. Since the coefficients have been changed, the K expression will be written differently and the K_c value will have to be changed accordingly. When dividing all coefficients by 2, the new form of the reaction has a K_c value that is raised to the ½ power. That is to say, when all the coefficients are divided by 2, the new K_c value is the square root of the old K_c value of 4.2 L/mol. Similarly, if all the coefficients are divided by 3, then the K_c value is raised to the ¹/₃ power; this is equivalent to taking the cube root of the original K_c power. Finally, if all the coefficients are multiplied by 5, the K_c value is raised to the 5^th power.
   
 
 

The Meaning of K

The numerical value of K provides an indicator of the extent to which a reaction occurs. Knowing that K is equal to the equilibrium concentrations of products divided by the equilibrium concentrations of reactants helps a student reason through the extent to which reactants turn to products. Let’s consider the generic reaction involving two reactant molecules and two product molecules:
   
Let’s suppose that we know that the K value for this reaction is 16. And let’s suppose we start with equal amounts of the two reactants and no products as depicted in the particle diagram. For simplicity, we could assume that each particle represents 1 mole and that the volume of the container is 1 L. This allows us to determine molar concentrations from a count of the number of particles.
 
To what extent will those reactants turn to products? Will half of the reactants form products? Will all of the reactants form products? Will 90% of them form products? One approach the problem is a trial-and-error approach. We can turn one or two of the reactant particles to products, count the numbers, and calculate the ratio of product to reactant amounts to see if the ratio equals the K value of 16. This is shown below with three trial-and-error iterations. On the third iteration, after having turned 8 of each of the original 10 reactant molecules to products, the equilibrium condition was satisfied with the ratio of product concentrations to reactant concentrations equaling the K value.
   
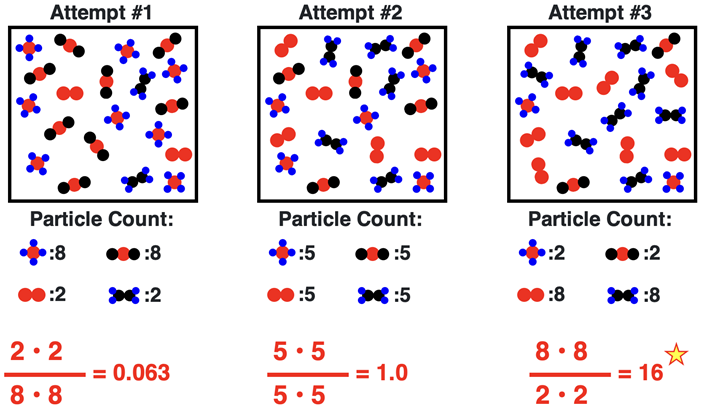
It isn’t difficult to imagine how the results of this trial-and-error process would change if the K value was different. For instance, if the K value was 0.0123, 0.0625, 1.00, or 81, the extent to which the reactants turn to products would be considerably different. The particle diagrams show the equilibrium positions achieved by the system for each of these K values, beginning with the same initial conditions of 10 particles of each reactant.
   

Clearly the equilibrium position changes when the K value changes. We can reason towards the following generalities.
 

• If K = 1, then the numerator = denominator; [products] = [reactants]
• If K >>> 1, then the numerator >>> denominator; [products] >>> [reactants]
• If K <<< 1, then the numerator <<< denominator; [products] <<< [reactants]

   
The K value provides a measure to which a reaction proceeds towards completion. A very small K indicates that the extent to which the reaction occurs is very low. A very large K value indicates that the reaction proceeds nearly to completion. And a K value that is equal to 1 indicates that the equilibrium position is characterized by nearly equal amounts of reactants and products. The discussion can become more complicated when …
 

• There are unequal exponents on the concentration values in the equilibrium expression.
• There are an unequal number of gaseous and aqueous-state reactant and product particles.
• There is initially an unequal number of each type of reactant particle.

 
In general, the K value provides a measure of the extent to which the reaction occurs.


  
 

Learning the Language of Equilibrium

A different collection of terms emerges when discussing reversible systems. Success requires that a student becomes familiar with the meaning of these terms. We introduced a few terms (proceeds to the left or proceeds to the right) on the previous page of Lesson 2. A few more terms arise on this page that are relevant to the discussion of the K value. They include:
 

• The equilibrium position lies to the right (or the equilibrium position lies on the product side).
• The equilibrium favors the formation of products.
• The equilibrium position lies to the left (or the equilibrium position lies on the reactant side).
• The equilibrium favors the formation of reactants.

 
When the K value is much greater than 1.0, it is common to say that the equilibrium position lies to the right or lies on the product side. This means that once equilibrium is established, the products are more prevalent than the reactants. We might also say that the equilibrium favors the formation of products.
 
On the other hand, it might be said that the equilibrium position lies to the left or lies on the reactant side when there is a K value much smaller than 1.0. This means that once equilibrium is established, the reactants are more prevalent than the products. We might also say that the equilibrium favors the formation of reactants.
 
 
 

Next Up

On the next page of Lesson 2, we will learn how to use equilibrium constant equations to calculate and equilibrium constant or an unknown equilibrium concentration. But before you click forward, take some time to internalize the concepts on this page using the suggestions in the Before You Leave section.
 
 
 

Before You Leave - Practice and Reinforcement

Now that you've done the reading, take some time to strengthen your understanding and to put the ideas into practice. Here's some suggestions.

• Try our Concept Builder titled Equilibrium Constant Expression. Any one of the three activities provides a great follow-up to this lesson.
• Try our Concept Builder titled The Equilibrium Concept. The third of the three activities provides a great follow-up to the meaning of a K value and the lingo used to describe the equilibrium position.
• The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.
• Download our Study Card on the Equilibrium Constant Expression. Save it to a safe location and use it as a review tool.

 
 
 
 

Check Your Understanding of Equilibrium Constant Expressions

Use the following questions to assess your understanding of how to write equilibrium constant expressions. Tap the Check Answer buttons when ready.
 
1. TRUE   or   FALSE:
The value of K depends upon the temperature of the system.

 
2. TRUE   or   FALSE:
For a given reaction system, if the equilibrium concentrations of reactants and products change, then the value of K will change.

​

 
3. The K_p value is often used instead of the K_c value when ____.
a. the reaction is rather explosive
b. the reactants and products are gases
c. there is no way to measure a concentration
d. the coefficients in the balanced chemical equation are 1

​

 
4. Write equilibrium constant equations (K_c) for the following reactions:
a.   CO(g)  +  3 H₂(g)    ⇄    CH₄(g)  +  H₂O(g)

​

 
b.   Ba(OH)₂(s)    ⇄    Ba²⁺(aq)  +  2 OH^-(aq)

​

 
c.   2 H₂S(g)  +  3 O₂(g)    ⇄    2 SO₂(g)  +  2 H₂O(l)

​

 
d.   2NO₃^-(aq)  +  8H⁺(aq)  +  3 Cu(s)    ⇄    2NO(g)  +  3Cu²⁺(aq)  +  4H₂O(l)

​

 
e.   HOCl(aq)     ⇄    H⁺(aq)  +  OCl^-(aq)

​

 

5. Use partial pressures to write equilibrium constant equations (Kp_c) for the following reactions:
a.   CO(g)  +  3 H₂(g)    ⇄    CH₄(g)  +  H₂O(g)

​

 
b.   2 HI(g)    ⇄    H₂(g)  +  I₂(s)

​

 
c.   N₂(g)  +   O₂(g)    ⇄    2 NO(g)
 
​

 

 
6. Consider the following generic reaction:
 
A(g)  +  3 B(g)  ⇄  2 C(g)  +  D(g)
 
What would be the units on K_c?

​

 

7. Consider the following generic reaction:
 
A(s)  +  3 B(aq)  ⇄  2 C(l)  +  D(g)
 
What would be the units on K_c?

​

 

8. Consider the reversible reaction: 2 X_2(g) + 3 Y_(g) ⇄ X₄Y_3(g)
The equilibrium constant at a certain temperature is 5.77 x 10^-2. Determine the equilibrium constant for the following reactions:

a. 4 X_2(g)  +  6 Y_(g)    ⇄  2 X₄Y_3(g)

​

 

b. X₄Y_3(g)    ⇄    2 X_2(g)   +   3 Y_(g)

​

 

c. 2 X₄Y_3(g)    ⇄    4 X_2(g)   +   6 Y_(g)

​

 

9. Consider the particle diagram for a reversible reaction system and three possible equilibrium positions. The particle diagrams below represent the mixture of reactants and products present at equilibrium for three different temperatures.
   
a. For which diagram is the K value very large (K >>> 1)?

​

 

b. For which diagram is the K value very small (K <<< 1)?

​

 

c. For which diagram is the K value approximately 1 (K = ~1)?

​

 

 

 
10. Consider the reversible reaction:   R     ⇄    B
 
A particle diagram of the system in the initial state and the equilibrium state is shown:
   
Which of the following are TRUE of this reversible system? Select all that apply.
a.    The equilibrium position lies to the right.
b.    The equilibrium favors the formation of products.
c.     The equilibrium constant is relatively small (K < 1).
d.    Given the initial composition, the reaction proceeds to the left to reach equilibrium.

​

 
 
11. Consider a reversible system:          R_(g)    ⇄    G_(g)
The Concentration-Time graphs for three such systems is shown. One of these systems is not like the others. For instance, two have a large K (the equilibrium position lies far to the right) while the other has a small K ... or vice versa. In terms of their K value, which one doesn't belong?  

​

 

 
12. Consider a reversible system:
 
A_(g)    ⇄    B_(g)
 
The value of K = 4.5. The initial conditions show that [B] / [A] = 9.2. Which of the following would be expected to occur in order for the system to reach an equilibrium state? Select all that apply.

1. The [A] increases and the [B] decreases.
2. The [A] decreases and the [B] increases.
3. The reaction proceeds in the forward direction (to the right).
4. The reaction proceeds in the reverse direction (to the left).

​