Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Lesson 2: Equilibrium
Part e: Analyzing Equilibrium Systems
Part a:
The Equilibrium State
Part b:
Equilibrium Constant Expressions
Part c:
Calculations of K and Concentration
Part d:
Predicting the Direction of Reaction
Part e: Analyzing Equilibrium Systems
From Initial to Equilibrium Concentrations
Lesson 2 of Chapter 14 of our Chemistry Tutorial has described the concept of equilibrium, has explained how to write an equilibrium constant equation, and has discussed how to predict the direction that a reversible system would proceed to reach an equilibrium. In this last part of Lesson 2, these ideas come together as you learn how to calculate the equilibrium concentrations that would result from a given set of initial concentrations. This will be a very problem-centered page with example problems accompanied by detailed solutions and practice problems that allow you to check your answers and view solutions. The problems will require the ability to manipulate an algebra equation to solve for an unknown variable.
ICE Tables
The task of determining the set of equilibrium concentrations that result from the initial conditions is facilitated by the use of an ICE table. ICE is an acronym for Inititial, Change, and Equilibrium. Each letter describes one of the three rows of the ICE table. The I or Initial row displays values of the initial concentration (or partial pressure) of all reactants and products in the chemical equation. The E or Equilibrium row displays values of the equilibrium concentration (or partial pressure) of all reactants and products in the chemical equation. The C or Change row indicates by how much the concentration (or partial pressure) changed between the initial and the equilibrium state. One or more rows will use a variable like x or 2x to represent an unknown quantity. The solution to a typical problem relies on the use of the ICE table to solve for the variable’s value.
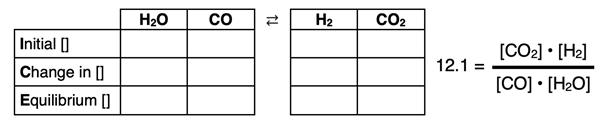
The graphic at the right represents an ICE table used for the reaction
H2O(g) + CO(g) ⇄ H2(g) + CO2(g)
There is a column in the ICE table for each reactant and product. The reactant columns are to the left of the reaction symbol ⇄. The product columns are on the right. Known values of concentration or partial pressures are entered into the table. The variable x is used at any location that a quantity is not known. The Equilibrium row of values (or algebraic expressions) are substituted into the equilibrium constant equation. The equation is then used to solve for x and for the unknown quantity. The best way to learn how to use an ICE table is to view examples of one being used to solve a problem and then to try a few problems in which you rely on an ICE table to solve the problem. We have five worked out examples below. There are plenty of practice opportunities described in the Before You Leave section near the bottom of the page.
Example 1
Consider the reversible system below.
H2O(g) + CO(g) ⇄ H2(g) + CO2(g)
The Kc value is 12.1. The reaction vessel is prepared with initial concentrations of reactants of 0.250 M. There are no products initially present. Determine all equilibrium concentrations.
Solution
Begin by sketching out an ICE table. Label the rows with I-C-E. And label the columns with the formulae of the reactants and products. Your table will be used to organize your solution. Because you will almost always need it, write the equilibrium constant equation for the reaction. This is shown below:
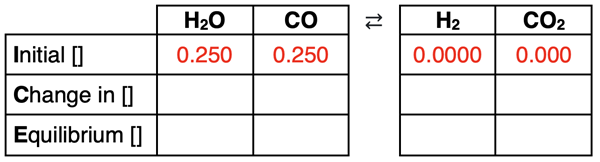
Now it’s time to use given values to fill in the table. Initial concentrations are given – 0.250 M for both reactants and 0.000 M for the products. These values are entered into the Initial row of the table.
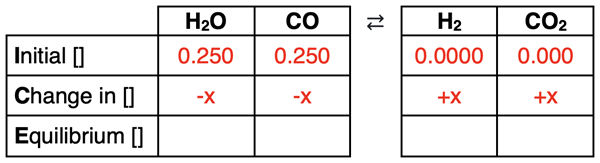
The reaction will proceed to the right, reacting away reactants and producing products. There is no way to know how much reactants react away or how much products formed; the variable x will have to be used to represent this. The coefficients in the balanced chemical equation always relate the change amount for the columns of the table. In this reaction, the coefficients are all 1. So, the amount of change will be the same for every reactant and product. But the reactants have a negative change (a decrease in concentration) and the products have a positive change (an increase in concentration). A -x will be used for the change in reactant concentrations and a +x will be used for a change in product concentrations.
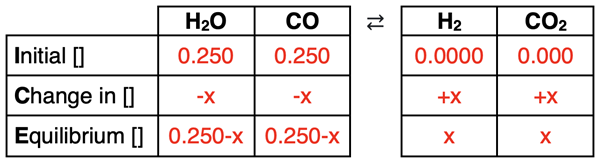
For each individual column, the equilibrium row is always equal to the initial row plus the change row. Because the change row often contains a variable x, the equilibrium row is often an expression rather than a number. Complete the Equilibrium row by adding the contents of the Initial and the Change rows.
At this point, there is one unknown – x. All that is needed is one equation to solve for that unknown. The equilibrium constant equation will be the equation we use to solve for x. The expressions for the equilibrium concentrations can be substituted into the equation.
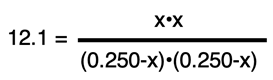
The chemistry problem has become an algebra problem. The solution will involve algebraically manipulating the equation to determine the value of x. There is more than one way to do this. Our approach will be to take the square root of each side. This simplifies the equation as shown.
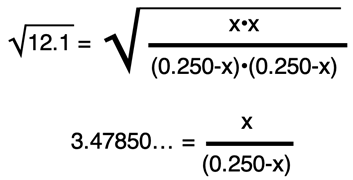
The algebraic goal is to now organize all the x terms in the equation by themselves on the same side of the equation. To do so, both sides of the equation will be multiplied by (0.250-x). This eliminates the denominator on the right side of the equation.
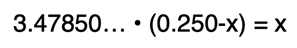
On the left side, both terms inside the parenthesis will be multiplied by the constant 3.47850 … (square root of 12.1) to produce
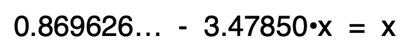
Adding the 3.47850•x term to each side of the equation will eliminate it from the left side and accomplish the goal of grouping x terms by themselves on one side. The two x terms can then be combined into one x term.
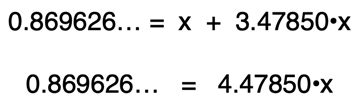
Dividing both sides of the equation by the coefficient in front of x allows us to determine the value of x.
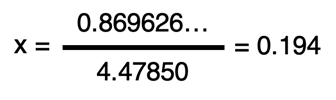
That was a lot of algebra work! Take a deep breath and get ready for the last step.
With x known, we can return to the last row of the ICE table and determine the equilibrium concentrations. For the reactants, the concentrations would be 0.250 - x. And for the products, the concentrations will be x. Thus, the equilibrium concentrations are
[H2O] = [CO] = 0.250 – x = 0.250 – 0.194 = 0.056 M
[H2] = [CO2] = x = 0.194 M
This multi-step problem involved an initial system that consisted of only reactants. Now we will consider the opposite case – the same reaction but initially only products. Our solution will be a bit briefer as we combine several steps along the way.
Example 2
Consider the reversible system below.
H2O(g) + CO(g) ⇄ H2(g) + CO2(g)
The Kc value is 12.1. The reaction vessel is prepared with initial concentrations of products of 0.250 M. There are no reactants initially present. Determine all equilibrium concentrations.
Solution
As before, we will begin by constructing an ICE table for each reactant and product and writing the equilibrium constant equation:
The initial row of the ICE table will include 0.000 M for reactant concentrations and 0.250 M for product concentrations. Since there are no reactants, the system will proceed to the left to reach equilibrium. This means that the reactants will have the positive change (+x) and the products will have the negative change (-x). As will always be the case, the values listed in the Equilibrium row are the Initial row values plus the Change row values or variables. The completed ICE table is shown below:
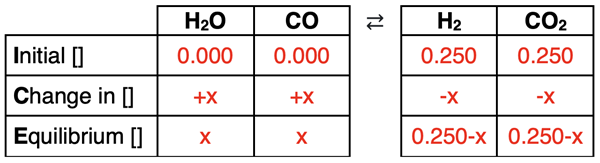
At this point, the problem becomes very algebraic in nature. The expressions for the equilibrium concentrations are substituted into the Kc equation. Then a collection of algebraic manipulations are performed to determine X. We have annotated the steps to this process below (in red):
The value of x is 0.056. This value can be substituted into the expressions for the Equilibrium row of the ICE table to determine the equilibrium concentrations.
[H2O] = [CO] = x = 0.056 M
[H2] = [CO2] = 0.250 – x = 0.250 – 0.056 = 0.194 M
In our third example, we will start with a mix of reactants and products. This adds a step of complexity. Before completing the Change row of the ICE table, a reaction quotient must be used to determine the direction that the reaction will progress to reach completion.
Example 3
Consider the reversible system below.
H2O(g) + CO(g) ⇄ H2(g) + CO2(g)
The Kc value is 12.1. The reaction vessel is prepared with both reactants and products. Each has an initial concentrations of 0.250 M. Determine all equilibrium concentrations.
Solution
The Initial row of the ICE table will display 0.250 for all reactants and products. The reaction quotient can be calculated and compared to the K value.
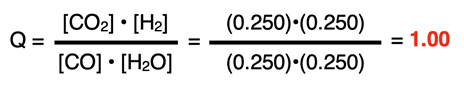
The Q value (1.00) is less than the K value (12.1). The reaction will proceed to the right, producing products and reacting away reactants. The reactants will have a negative change in concentration and the products will have a positive change in concentration. Whenever a problem provides initial concentrations for all reactants and products, this is the necessary first step - to determine the Q and to compare it to the K value.
The ICE table can now be completed.
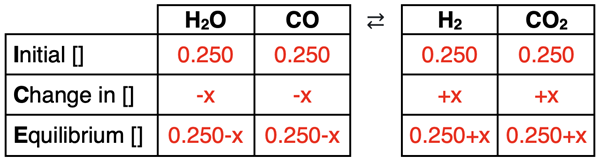
The four expressions for the equilibrium concentrations (bottom row) can be substituted into the Kc equation. This will results in a relatively complex algebra equation. Through a number of steps, the value of x can be determined. Each step is annotated below.
The value of x is determined to be 0.138. This value can be substituted into the expressions in the equilibrium row of the ICE table.
[H2O] = [CO] = 0.250 - x = 0.250 – 0.138 = 0.112 M
[H2] = [CO2] = 0.250 + x = 0.250 + 0.138 = 0.388 M
We have now seen three examples showing how to use the ICE table and the K
c equation to determine an x value and ultimately the equilibrium concentrations. In Example 4, we will analyze a different reaction system and use a K
p value instead of a K
c value.
Example 4
Consider the reversible system below.
N2O4(g) ⇄ 2 NO2(g)
The Kp value is 0.175. The reaction vessel is prepared with both reactants and products. The partial pressure of N2O4 is 1.08 atm. The partial pressure of NO2 is 2.42 atm. Determine all equilibrium partial pressures.
Solution
Like the previous three examples, an ICE table will be used to organize the information. The ICE table will list pressures (P) instead of concentrations ([ ]). The table will include one column for the reactant and one column for the product. A pressure equilibrium constant equation will also need to be written and used. Here’s the set-up of the table and the equation:
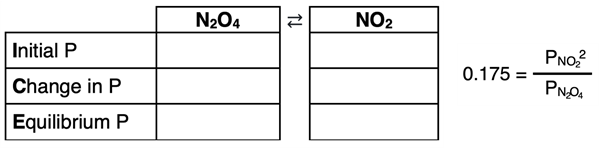
Since both reactant and the product are initially present, a reaction quotient must be used to determine the direction that the reaction proceeds.
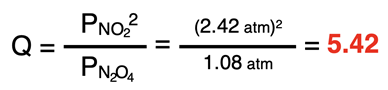
The reaction quotient (5.42) is larger than the Kp value (0.175). Thus, the reaction proceeds to the left, increasing the partial pressure of N2O4 and decreasing the partial pressure of NO2. The ICE table can now be completed.
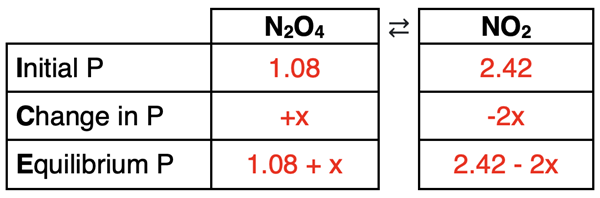
You will notice that the amount of change of NO2 is twice the amount of change for N2O4. This is because of the coefficient 2 in front of the formula. The Change row of the ICE table always reflects the mole ratios of the balanced chemical equation (and in this case, the pressure ratios).
The expressions for the equilibrium pressure can be substituted into the Kp equation. A lot of algebra follows in the attempt to solve for x. All algebraic steps are briefly described below.
The algebraic pathway to determining x results in a quadratic equation. There are two possible solutions to the equation. One of the possible x values (1.54915) can be ruled out since its use in the equilibrium pressure of NO2 would result in a negative pressure value. The other x value – 0.914596 will be used.
The equilibrium pressures of the two gases are
P of N2O4 = 1.08 + x = 1.08 + 0.914596 = 1.99 atm
P of NO2 = 2.42 – 2x x = 2.42 – 2•(0.914596) = 0.59 atm
Example 5
Consider the reversible system below.
H2(g) + I2(g) ⇄ 2 HI(g)
The Kc value is 6.25. The system is initially prepared by adding 0.500 mol of each reactant gas to a 2.00-L reaction vessel.
Solution
The solution begins by constructing an ICE table for the reaction and writing the Kc equation.
The initial concentrations in mol/L are 0.250 M for each reactant. This is determined by dividing the number of moles (0.500) by the volume (2.00 L). Since no product is initially present, the reaction will proceed to the right. We will use a “-x” to describe the change in reactant concentrations and a “+2x” to describe the change in product concentration. The 2 in +2x is the coefficient in front of the product. The completed ICE table is shown below.
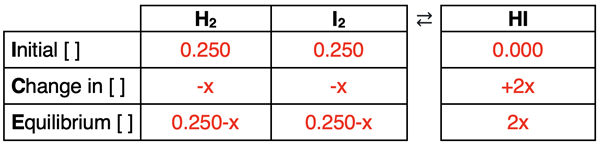
The expressions for the equilibrium concentrations are now substituted into the Kc equation. Then a collection of algebraic manipulations are performed to determine x. Each step is annotated below.
The value of x is determined to be 0.1388888… . This value can be substituted into the expressions in the equilibrium row of the ICE table.
[H2] = [I2] = 0.250 - x = 0.250 – 0.1388888 = 0.111 M
[HI] = 2•x = 2•(0.138888) = 0.278 M
It is important to view solutions to these difficult problems. But viewing another person’s solution to a problem is not a substitute for practice. There are several suggestions in the
Before You Leave section that will provide important practice opportunities.
Before You Leave
- Try our Concept Builder titled Equilibrium ICE Tables. Any one of the three activities will help you learn how to use ICE Tables.
- Our Calculator Pad section is the go-to location to practice solving problems. You’ll find plenty of practice problems on our Kinetics and Equilibrium page. Check out the following problem sets: ICE Tables 1 || ICE Tables 2
- Download our Study Card on ICE Tables. Save it to a safe location and use it as a review tool. (Coming Soon.)
- The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.
Check Your Understanding
Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
For Questions #1-3: The homework has been collected, and the following examples of NOT NICE ICE were found. Identify what is wrong with the following ICE table and Kc set ups. Many of the examples have more than one error; find them all.
1. Problem:
The Kc of the following reversible system is 0.0250.
2 H2S (g) ⇄ 2 H2(g) + S2(g)
The initial concentration of H2S is 0.500 M. Determine the equilibrium concentrations.
ICE and Kc set up:
2. Problem:
The K
p of the following reversible system is 0.360.
N2(g) + 3 H2(g) ⇄ 2 NH3(g)
The initial partial pressures of the two reactants are 2.00 atm each. There is no product present. Determine the equilibrium partial pressures.
ICE and Kc set up:
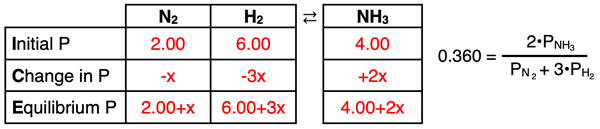
3. A Problem:
The K
c of the following reversible system is 16.0.
Cl2(g) + 2 Br-(aq) ⇄ Br2(l) + 2 Cl-(aq)
The initial concentrations of Cl2 and Br- are 0.010 M and 0.200 M, respectively. Determine the equilibrium concentrations.
ICE and Kc set up:
4. Consider the reversible system below.
H2O(g) + CO(g) ⇄ H2(g) + CO2(g)
The initial concentrations of the reactants are 1.20 M each. There are initially no products. At a certain temperature, the equilibrium concentration of H2O is determined to be 0.35 M.
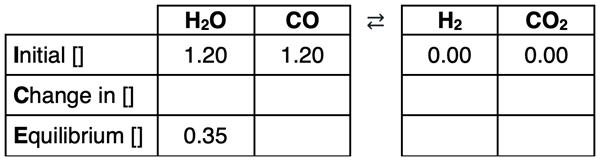
Complete the remainder of the ICE table and determine the Kc value at this temperature. (HINT: There is no need for an x in this problem. All cells of the table should have numerical values.)
5. Consider the reversible system below.
H2(g) + I2(g) ⇄ 2 HI(g)
The Kc value is 6.25. The system is initially prepared by adding 0.100 mol of each reactant gas and 0.400 mol of the product gas to a 2.00-L reaction vessel.
a. Determine the initial concentrations of all reactants and the product.
b. Calculate a reaction quotient and determine the direction that the reaction proceeds on its way to equilibrium.
c. Set up and organize the solution to this problem using an ICE table.
d. Substitute expressions for the equilibrium concentrations into a K
c equation and solve for x.
e. Calculate the equilibrium concentrations of the reactants and the product.
NOTE: Additional practice ideas can be found in
the Before You Leave section above.