Lesson 2: Equilibrium

Part d: Predicting the Direction of Reaction

Part a: The Equilibrium State
Part b: Equilibrium Constant Expressions
Part c: Calculations of K and Concentration
Part d: Predicting the Direction of Reaction
Part e: Analyzing Equilibrium Systems

 

The Big Idea

By calculating the reaction quotient (Q) and comparing it with the equilibrium constant (K), you can predict whether the system will move toward reactants or products in order to reach equilibrium.

 

Which Way to Equilibrium?

Lesson 2 has been all about reversible reaction systems and their tendency to change concentrations until an equilibrium is established. We’ve learned that reversible systems will establish equilibrium regardless of the starting conditions. Such systems react in either direction - reactants form products (the usual) and products can form reactants. So even a system that starts with all products will be able to proceed towards an equilibrium position with a mix of reactants and products because the reaction works in reverse.
 
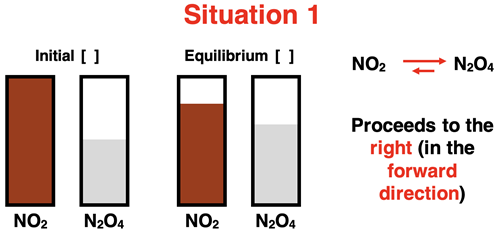
This idea was first introduced in Lesson 2a when discussing a variety of possible equilibrium positions for the NO₂ - N₂O₄ reversible system:

2 NO₂(g)   ⇄   N₂O₄(g)

We considered a variety of initial conditions and observed how sometimes the reaction proceeded to the right to increase the product concentrations and at other times the reaction proceeded to the left to increase reactant concentrations. For the initial conditions in Situation 1, the reaction proceeds to the right. To reach equilibrium, the system responds to the initial conditions by increasing the amount of N₂O₄ and decreasing the amount of NO₂. That is, the system initially produces N₂O₄ at a faster rate than it produces NO₂, eventually achieving an equilibrium with increased [N₂O₄] and decreased [NO₂].

 
 
The system responds differently to the initial conditions of Situation 2. The system proceeds in the direction of the reactant NO₂. That is, the system initially produces NO₂ at a faster rate than it produces N₂O₄, eventually achieving an equilibrium with increased [NO₂] and decreased [N₂O₄].

 
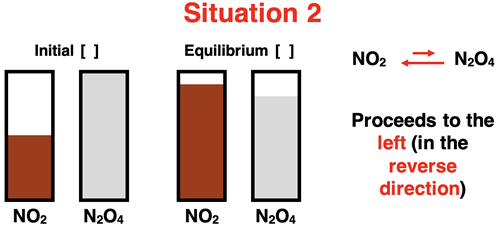
The question we wish to answer in Lesson 2d is: What rule allows one to predict the direction that a reversible system will proceed in order to reach equilibrium? The prediction is easy for conditions in which there is either no reactant or no product. But when the initial conditions include a mix of reactants and products, there must be a rule that can be used to predict the direction a reaction proceeds. We will soon learn that rule!

 

 
 

What is a Reaction Quotient?

An equilbrium constant expression (like the one shown at the right) can be written for any reversible system based on the balanced chemical equation. If equilibrium concentrations are substituted into the expression, then one is calculating an equilibrium constant. This was one of the two topics of Lesson 2c. But if the initial concentrations (or concentrations at any instant) are substituted into the same expression, then one is calculating the reaction quotient (Q). The reaction quotient provides a rough indicator of how close a system is to equilibrium. The closer that the value Q is to K, the closer that the system is to equilbrium. That is, as concentrations for a reversible system change, the value of Q will change so as to approach the value of K. Once Q equals K, the system is at equilibrium.

 
But the value of Q also indicates to what side of equilibrium that the reaction is initially (or currently) at. The equilbrium expression lists the product concentrations over the reactant concentrations (with their appropriate exponents). If the value of Q is initially less than the value of K, then there are too few products and too much reactants. Such a system will proceed to the right (towards products) to reach equilibrium. On the other hand, if the value of Q is initially greater than K, there then are too many products and too few reactants. The system will proceed to the left (towards reactants) to reach equilibrium.

 
So, to make a prediction as to which direction a reaction proceeds to reach equilibrium, the value of Q must be calculated using currently known concentrations. By comparing this Q value to the K value, one can decide which direction the reaction proceeds - towards products (to the right) or towards reactants (to the left) - in order to reach equilibrium. The following step-by-step procedure details the process. It assumes that the K_c value is known and the concentrations at some instant in time are known.

1. Write the equilibrium constant expression for the given reaction.
2. Substitute known concentration values into the expression and calculate Q.
3. Compare the Q value to the K value and decide on the direction.

• If Q < K, then the reaction proceeds to the right (towards products)
• If Q > K, then the reaction proceeds to the left (towards reactants)

   
 

Example 1 - Predicting the Direction a Reaction Proceeds

At a specific temperature, the reaction
   
has a K_c value of 5.2. Suppose that the following concentrations are known:
   
Which direction will the system proceed to reach equilibrium? And how will this direction affect each of the concentrations?
 
 

Solution:

First an equilibrium expression is written for the reaction (top row below). Then the known concentrations are substituted into the expression to calculate the Q value (second row). This Q value (2.60) is compared to the K_c value (5.2).  
Since the Q is less than the K_c value, the reaction proceeds to the right. Because the reaction proceeds to the right (in the direction of products), one would expect the reactant concentrations to decrease and the product concentrations to increase.
 
As these concentrations changes occur, the value of Q will increase until finally it is equal to the value of K. At that point equilibrium is said to be established and the concentrations will no longer change.
   
 

Example 2 - Predicting the Direction a Reaction Proceeds

At a specific temperature, the reaction system
   
has an equilibrium constant (K_c) of 2.46. The following concentrations are known:
 
Which direction will the system proceed to reach equilibrium? And how will this direction affect each of the concentrations?
 
 

Solution:

First an equilibrium expression is written for the reaction (top row below). Then the known concentrations are substituted into the expression to calculate the Q value (second row). This Q value (7.14) is compared to the K_c value (2.46).  
Since the Q is greater than the K_c value, the reaction proceeds to the left. Because the reaction proceeds to the left (in the direction of reactants), one would expect the reactant concentrations to increase and the product concentrations to decrease.
 
 As these concentrations changes occur, the value of Q will decrease until finally it is equal to the value of K. At that point equilibrium is said to be established and the concentrations will no longer change.
 
 
 
 

Example 3 - Predicting the Direction a Reaction Proceeds

Consider the reversible system
   
with a K_c value of 502. Given the following initial conditions:
 
indicate the direction in which the reaction proceeds to reach equilibrium. What effect will this have on the concentrations of each reactant and the product?
 
 

Solution:

First an equilibrium expression is written for the reaction (top row below). Then the known concentrations are substituted into the expression to calculate the Q value (second row). This Q value (88) is compared to the K_c value (502).  
Since the Q is less than the K_c value, the reaction proceeds to the right. Because the reaction proceeds to the right (in the direction of products), one would expect the reactant concentrations to decrease and the product concentrations to increase.
 
As these concentrations changes occur, the value of Q will increase until finally it is equal to the value of K. At that point equilibrium is said to be established and the concentrations will no longer change.
 
 

 

Before You Leave - Practice and Reinforcement

Now that you've done the reading, take some time to strengthen your understanding and to put the ideas into practice. Here's some suggestions.

• Our Calculator Pad section is the go-to location to practice solving problems. You’ll find plenty of practice problems on our Kinetics and Equilibrium page. Check out the following problem set:  Problem Set KE13: Reaction Quotient and Direction of Reaction
• The Check Your Understanding section below include questions with answers and explanations. It provides a great chance to self-assess your understanding.
• Download our Study Card on Direction of the Reaction. Save it to a safe location and use it as a review tool.

 
 
 
 

Check Your Understanding the Direction that a Reaction Proceeds

Use the following questions to assess your understanding of how to predict the direction that a reaction proceeds iniorder to reach an equilibrium state. Tap the Check Answer buttons when ready.
 
1. A system will proceed to the right to reach an equilibrium state if ….

1. the reactant concentrations are greater than the product concentrations.
2. the product concentrations are greater than the reactant concentrations.
3. Come on now! Don’t over-complicate matters. A reaction can do whatever it wants to do. It’s Chemistry after all.
4. Nonsense. It’s not that simple. You need to know the K value and calculate the Q value and do a comparison. It’s complicated. But you got this!

 


 
For Questions #2-4:
Consider the reaction:  X₂(g)   +   Y₂(g)  ⇄   2 XY(g)
The equilibrium constant (K_c) is 0.335.  A vessel of X₂, Y₂, and XY is mixed, with each gas having a concentration of 0.050 M.
 
2. Calculate the value of the reaction quotient (Q) immediately after mixing.
 


 
3. Which of the following must occur for the reaction mixture to reach equilibrium?

1. The X₂ and Y₂ concentrations must increase and the XY concentrations must decrease.
2. The X₂ and Y₂ concentrations must decrease and the XY concentrations must increase.
3. Nonsense! The system is already at equilibrium

 


 
4. How will the system behave to reach equilibrium?

1. The reaction will proceed to the right to produce additional products.
2. The reaction will proceed to the left to produce additional reactants.
3. Nonsense! The system is already at equilibrium and amounts of reactants and products will not change.

 

 

 
 
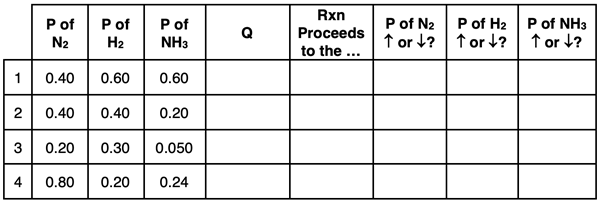
5. Consider the following reversible reaction system shown below.

N₂(g)    +    3 H₂(g)      ⇄    2 NH₃(g)

At a particular temperature, the K_p value is 2.5.  For each of the following sets of initial conditions, calculate Q and determine which direction the reaction proceeds to reach equilibrium.  For each row, indicate what happens to the partial pressures of the three gases as a result of this ongoing change.